Резонанс напряжений
Резонанс (франц. résonance, от лат. resono – откликаюсь), резкое возрастание амплитуды колебаний системы по мере приближения частоты вынужденных (сторонних) колебаний системы к частоте её собственных колебаний. Приведём случай резонанса, имевший место в XIX cтолетии. Рота русских солдат переходила в ногу деревянный мост через речушку Мойка (одна из проток Невы в Санкт-Петербурге). Под ударами ног мост стал всё сильней раскачиваться, и в конце концов рухнул в воду. Дело было летом, никто из солдат не простыл. «Виновник» случившегося – резонанс, причина которого состояла в следующем: частота ударов ног солдат о поверхность моста совпала с частотой собственных колебаний моста. Последняя зависела от конструкции моста и размеров его деталей. С тех пор во всём мире принято правило: группы военнослужащих переходят мосты не в ногу. Ещё один пример. При настройке на определенную радиостанцию вы вращаете рукоятку настройки, связанную с пластинами конденсатора переменной ёмкости внутри радиоприёмника. По мере приближения к волне, на которой работает радиостанция, громкость постепенно усиливается и становится максимальной в момент настройки радиоприёмника на упомянутую стабильную волну. В данном примере, вращая рукоятку настройки, Вы частоту собственных колебаний Явление резонанса возможно в цепи, в которой катушка и конденсатор соединены последовательно или параллельно. Резонанс при последовательном соединении называется резонансом напряжений, при параллельном – резонансом токов. Однако, независимо от вида резонанса, условие резонанса всегда одно и то же, а именно: частота собственных колебаний цепи
В свою очередь, частота собственных колебаний цепи зависит только от значений её индуктивности
где
С – ёмкость конденсатора, Ф. Рассмотрим особенности резонанса напряжений (рис. 6.65). Путём соответствующих преобразований можно перейти от равенства (6.200) к такому равенству:
Смысл последнего состоит в следующем: резонанс напряжений наступает при равенстве индуктивного и ёмкостного сопротивлений цепи. Иначе говоря, при наступлении резонанса реактивное сопротивление цепи
В этом случае ток в цепи ограничивается только её активным сопротивлением:
и в момент резонанса достигает своего максимально возможного значения.
Рис. 6.65. Векторная (а) и волновая (б) диаграммы напряжений и токов при резонансе напряжений
На векторной диаграмме реактивное напряжение Иначе говоря, при резонансе напряжений цепь ведёт себя как цепь с одним только активным сопротивлением При этом катушка и конденсатор периодически обмениваются реактивной энергией, первоначально полученной от источника питания, а в резисторе происходит безвозвратное преобразование энергии источника питания в тепловую – резистор нагревается. Перенапряжения на катушке и конденсаторе при резонансе напряжений При резонансе напряжений возможны перенапряжения на катушке и конденсаторе. При резонансе напряжений падения напряжения на катушке и конденсаторе равны:
где
– т. н. добротность контура, т. е. число, показывающее, во сколько раз индуктивное или ёмкостное сопротивление цепи больше или меньше активного. Перенапряжения на катушке и конденсаторе наступают, если
|

 входного контура радиоприемника постепенно приближали к фиксированной частоте вынужденных колебаний
входного контура радиоприемника постепенно приближали к фиксированной частоте вынужденных колебаний  передающей радиостанции.
передающей радиостанции. и ёмкости С, и не зависит от напряжения или тока:
и ёмкости С, и не зависит от напряжения или тока: (6.201).
(6.201). , (6.202)
, (6.202) . (6.203)
. (6.203) (6.204)
(6.204)
 = 0, поэтому ток
= 0, поэтому ток 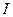 совпадает по фазе с напряжением питания
совпадает по фазе с напряжением питания  .
.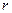 .
.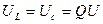 , (6.205)
, (6.205) (6.206)
(6.206) > 1.
> 1.


