Пример 6.97.
Рассчитать ёмкость конденсатора С, необходимую для настройки радиоприёмника на частоту Решение. 1. длина волны радиостанции, работающей на частоте
где С = 300*10 2. из (6.201) ёмкость конденсатора в момент резонанса
6.4. Трёхфазные цепи 6.4.1. Получение трёхфазного тока Для получения 3-фазного тока используются 3-фазные генераторы (рис. 6.68, а).
Рис. 6.68. Трёхфазный синхронный генератор; волновая (а) и векторная (б) диаграммы фазных ЭДС
На статоре такого генератора размещены три одинаковые фазные обмотки А-Х, В-Y и С-Z, сдвинутые по окружности на 120º. Каждую такую обмотку можно рассматривать как однофазный генератор, устройство и принцип действия которого был объяснен ранее (рис. 6.45, а). На роторе генератора находятся два полюса N и S с катушками постоянного тока. При вращении ротора генератора, например, по часовой стрелке, в каждой фазной обмотке индуктируется ЭДС одинаковой частоты и амплитуды. Однако одинаковые, например, максимальные положительные значения, эти ЭДС будут достигать не одновременно, а со сдвигом по времени. Последнее объясняется тем, что сами обмотки сдвинуты по окружности статора на угол 120º. Напомним, что максимальные значения ЭДС индуктируются в обмотке, если она расположена под срединой полюсов ротора. На рис. 6.68, а такая ЭДС наводится в обмотке А-Х (что не соответствует значениям этой ЭДС на волновой и векторной диаграммах – ну, Частоедов! Погоди!). Далее, по мере поворота ротора по часовой стрелке, максимальные значения ЭДС индуктируются в обмотке В-Y, а затем – в обмотке С-Z. Поэтому законы изменения ЭДС в фазных обмотках такие:
Волновые и векторные диаграммы этих ЭДС изображены на рис.6.68, а и б. В изображенной на рис. 6.68, а, фазные обмотки электрически не связаны друг с другом. Поэтому такая электрическая система называется несвязанной В такой системе для связи генератора с приёмниками электроэнергии ZA, ZB и ZC используются 6 проводов, что делает её неэкономичной. Поэтому на практике применяют более экономичные трёх- и четырёхпроводные системы 3-фазного переменного тока. Рассмотрим эти системы.
6.4.2. Соединение обмоток трёхфазного генератора звездой Схема соединения обмоток генератора звездой изображена на рис. 6.69.
Рис. 6.69. Схема соединения обмоток генератора звездой (а); векторная диаграмма фазных и линейных напряжений генератора (б)
Как следует из схемы, для получения звезды надо концы обмоток X, Y и Z соединить в общую точку N, к которой присоединён нейтральный провод. Эта точка называется нейтральной или нулевой. Начала А, В и С фазных обмоток присоединены к одноимённым линейным проводам А, В и С, а нулевая точка N – к нейтральному проводу Введём понятия «линейное» и «фазное» напряжения. Линейным называется напряжение между двумя линейными проводами. Таких напряжений три: Фазным называется напряжение между началом и концом одной и той же фазной обмотки. Таких напряжений три: между выводами А и Х – Поскольку выводы X, Y и Z соединены с нейтральной точкой N, можно сформулировать второе, равнозначное определение понятия «фазное напряжение», а именно: Фазным называется напряжение между началом фазной обмотки и нейтральным проводом. Например, фазное напряжение Для вывода соотношения между линейными и фазными напряжениями используются уравнения ŪАВ = ŪА – ŪВ (6.211) ŪВС = ŪВ – ŪС (6.212) ŪСА = ŪС – ŪА (6.213) На основании этих уравнений построена векторная диаграмма фазных и линейных напряжений (рис. 6.69, б), из которой следует:
Обратное соотношение:
|

 100 кГц, если индуктивность катушки входного контура приёмника
100 кГц, если индуктивность катушки входного контура приёмника 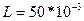 Гн. Схема – на рис. 6.67, а.
Гн. Схема – на рис. 6.67, а. =
=  = 3 м,
= 3 м,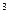 км/с – скорость света в вакууме (воздухе).
км/с – скорость света в вакууме (воздухе). =
=  ≈ 2*10-9 Ф = 2*10-3 мкФ.
≈ 2*10-9 Ф = 2*10-3 мкФ.

 (6.208)
(6.208) (6.209)
(6.209) (6.210).
(6.210).

 ,
, 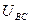 и
и  .
. , между выводами В и Y –
, между выводами В и Y –  , между выводами С и Z –
, между выводами С и Z –  .
. (6.214)
(6.214) (6.215).
(6.215).


