Гипотеза Кирхгоффа и ее следствия
Теория тонких пластин строится на основе гипотезы Кирхгоффа, сущность которой заключается в следующем: в процессе деформирования пластина в плоскостях, нормальных к ее срединной плоскости, ведет себя в отношении сдвигов и удлинений вдоль оси z как абсолютно твердое тело. Назовем отрезки, ортогональные срединной плоскости пластины и заключенные между граничными плоскостями нормали пластины не деформируются и остаются нормалями к ее срединной поверхности (деформированной срединной плоскости). В соответствии с этим гипотезу Кирхгоффа часто называют гипотезой о неизменяемости нормалей пластины. Следует подчеркнуть, что поводом для введения гипотезы Кирхгоффа послужили наличие у пластины малого геометрического параметра (толщины Обозначим через
Из первого уравнения (1.1) следует, что смещение
 на одну и ту же величину, получившую название прогиба пластины. Условимся в дальнейшем частные производные прогиба по пространственным координатам на одну и ту же величину, получившую название прогиба пластины. Условимся в дальнейшем частные производные прогиба по пространственным координатам  обозначать соответствующими индексами снизу. Например, обозначать соответствующими индексами снизу. Например,
Учитывая (1.2), из двух последних дифференциальных уравнений (1.1) имеем
представляют смещения точек срединной плоскости пластины вдоль осей  и и  соответственно. Они имеют место при деформировании пластины в ее плоскости, описываемом плоским напряженным состоянием. В теории изгиба пластин их можно положить равными нулю, что соответствует нерастяжимости срединной плоскости пластины при ее изгибе. Другими словами, задача об общем пространственном деформировании пластины слагается из задачи о ее плоском напряженном состоянии и изучаемой нами задачи изгиба пластины. Важно подчеркнуть, что названные две задачи независимые. Здесь уместно провести аналогию с теорией стержня, согласно которой задача об общем плоском деформировании прямолинейного стержня разбивается на две независимые задачи. Одна из них — задача о растяжении-сжатии стержня, а другая — задача о его поперечном изгибе. Проведенная аналогия наглядно иллюстрируется на рис. 1.2, где на рис. 1.2 а представлено отмеченное разделение для стержня, а на рис. 1.2 б — для пластины. соответственно. Они имеют место при деформировании пластины в ее плоскости, описываемом плоским напряженным состоянием. В теории изгиба пластин их можно положить равными нулю, что соответствует нерастяжимости срединной плоскости пластины при ее изгибе. Другими словами, задача об общем пространственном деформировании пластины слагается из задачи о ее плоском напряженном состоянии и изучаемой нами задачи изгиба пластины. Важно подчеркнуть, что названные две задачи независимые. Здесь уместно провести аналогию с теорией стержня, согласно которой задача об общем плоском деформировании прямолинейного стержня разбивается на две независимые задачи. Одна из них — задача о растяжении-сжатии стержня, а другая — задача о его поперечном изгибе. Проведенная аналогия наглядно иллюстрируется на рис. 1.2, где на рис. 1.2 а представлено отмеченное разделение для стержня, а на рис. 1.2 б — для пластины.
Таким образом, в теории изгиба пластины можно считать
 . .
Тем самым показана полная эквивалентность обеих формулировок гипотезы Кирхгоффа. Из (1.4) следует, что отличные от нуля компоненты пространственного тензора деформаций равны
 , исключая срединную. Характерно, что величина этих деформаций пропорциональна удаленности от срединной поверхности. Заметим также, что при деформировании пластины, все ее плоскости, нормальные оси , исключая срединную. Характерно, что величина этих деформаций пропорциональна удаленности от срединной поверхности. Заметим также, что при деформировании пластины, все ее плоскости, нормальные оси  остаются эквидистантными. остаются эквидистантными.
Итак, гипотеза Кирхгоффа позволила установить закон изменения смещений и деформаций по толщине пластины. Тем самым трехмерная геометрия деформирования пластины сведена к двухмерной, полностью описываемой единственной функцией двух переменных — прогибом пластины Принимая гипотезу Кирхгоффа, мы до сих пор ничего не сказали о том, чем эта гипотеза может быть обеспечена в полной и строгой модели трехмерной теории упругости при действии на пластину, вообще говоря, любых внешних нагрузок. Навязывая пластине условиями (1.1) недеформируемость в нормальных плоскостях, мы, по существу, наделяем ее материал специальными свойствами и тем самым вторгаемся в физическую сторону теории упругости. Эти рассуждения наводят на мысль — искать строгое модельное обоснование гипотезы Кирхгоффа именно в физической стороне. Ясно, что в рамках изотропного упругого тела такое обоснование недоступно, так как выражающие гипотезу Кирхгоффа математические зависимости (1.1) навязывают телу анизотропность и, как легко понять, в рамках частного вида анизотропии, известного под названием трансверсальной изотропии. Напомним физические соотношения трансверсально-изотропного тела, предполагая, что плоскость его изотропных упругих свойств перпендикулярна оси
Здесь Из последних соотношений видно, что независимо от характера внешнего нагружения для выполнения гипотезы Кирхгоффа (равенств (1.1)) необходимо и достаточно устремить к бесконечности модули
 , ,  и и 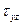 становятся неопределенными, и единственная возможность для раскрытия этой неопределенности предоставляется в статической стороне. становятся неопределенными, и единственная возможность для раскрытия этой неопределенности предоставляется в статической стороне.
Трансверсально-изотропный материал с неограниченными модулями Записывая уравнения (1.8) в обратной форме
с помощью (1.7) находим
 , ,  , , 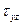 обратимся к пространственным уравнениям равновесия ( обратимся к пространственным уравнениям равновесия ( ) )
 . На них . На них  , ,  , ,  , , 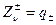 , так что , так что
где, как обычно, символом
Интегрируя предпоследнее равенство по
— статический момент отсеченной части прямоугольного сечения высотой Совершенно аналогично из (1.9) и второго уравнения (1.10) сначала находим равенство
а затем формулу
 . .
Наконец, из третьего уравнения равновесия (1.10) и формул (1.12), (1.13) имеем
Здесь введен бигармонический оператор
Интегрируя предпоследнее равенство в тех же пределах (от
Требуя теперь выполнения третьего условия (1.11) и при
и так называемая цилиндрическая жесткость пластины
 , через который выражены все смещения (см. (1.4)), деформации (см. (1.7)) и напряжения (см. (1.9), (1.12), (1.13), (1.14)). Заметим, что с учетом уравнения Софи Жермен формула (1.14) приобретает вид , через который выражены все смещения (см. (1.4)), деформации (см. (1.7)) и напряжения (см. (1.9), (1.12), (1.13), (1.14)). Заметим, что с учетом уравнения Софи Жермен формула (1.14) приобретает вид
где Подводя итоги, отметим, что упругие смещения
|

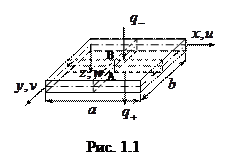 Ограничимся рассмотрением нагружения пластины нормальными поверхностными нагрузками
Ограничимся рассмотрением нагружения пластины нормальными поверхностными нагрузками  , приложенными соответственно к границам
, приложенными соответственно к границам  ) и основанные на эмпирических фактах интуитивные представления о малой деформируемости тонкой пластины по ее толщине.
) и основанные на эмпирических фактах интуитивные представления о малой деформируемости тонкой пластины по ее толщине.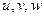 — декартовые компоненты вектора смещений, являющиеся, вообще говоря, функциями трех координат
— декартовые компоненты вектора смещений, являющиеся, вообще говоря, функциями трех координат  . Если теперь вспомнить соотношения Коши и смысл определяемых ими компонент деформаций, то недеформируемость пластины в нормальных ее плоскостях означает, что
. Если теперь вспомнить соотношения Коши и смысл определяемых ими компонент деформаций, то недеформируемость пластины в нормальных ее плоскостях означает, что
 не зависит от координаты
не зависит от координаты 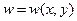
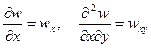








 ,
,  ,
, 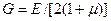 — упругие константы в плоскости изотропии,
— упругие константы в плоскости изотропии, 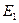 — модуль Юнга в направлении оси
— модуль Юнга в направлении оси  — модуль сдвига в нормальной плоскости пластины,
— модуль сдвига в нормальной плоскости пластины,  — коэффициент поперечного сжатия в плоскости изотропии при растяжении вдоль оси
— коэффициент поперечного сжатия в плоскости изотропии при растяжении вдоль оси 





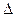 обозначен дифференциальный оператор Лапласа:
обозначен дифференциальный оператор Лапласа:
 до
до  получим
получим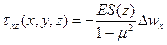



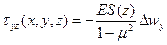




 , приходим к уравнению
, приходим к уравнению


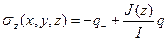
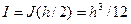 момент инерции сечения, показанного на рис 1.3, относительно его горизонтальной оси симметрии. Последняя формула показывает, что напряжение
момент инерции сечения, показанного на рис 1.3, относительно его горизонтальной оси симметрии. Последняя формула показывает, что напряжение 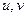 , упругие деформации
, упругие деформации  и напряжения
и напряжения  пластины изменяются по ее толщине по линейному закону (см. (1.4), (1.7), (1.9)), не упругие поперечные касательные напряжения
пластины изменяются по ее толщине по линейному закону (см. (1.4), (1.7), (1.9)), не упругие поперечные касательные напряжения  — по закону квадратной параболы (см. (1.12), (1.13)), а нормальные напряжения
— по закону квадратной параболы (см. (1.12), (1.13)), а нормальные напряжения 


