Поперечный изгиб круглых пластин
При изучении деформирования прямоугольных пластин естественным было использование декартовой системы отсчета. Залогом относительной простоты математических выкладок явилось то, что граничный контур пластины совпадал с координатными линиями этой системы. Если граничный контур пластины совпадает с полярными координатными линиями, то принципиально возможное применение декартовой системы отсчета влечет за собой неоправданные математические усложнения. Избежать их удается путем перехода к полярным координатам. Особенно отчетливо преимущества полярной системы координат проявляются при рассмотрении круглых пластин. 6.1. Основные соотношения теории изгиба пластин в полярных координатах. Теорию тонких пластин в полярных координатах можно было бы строить по образу и подобию теории в декартовой системе отсчета с соответствующей редакцией всех рассуждений на использование полярных координат. В этом, однако, нет необходимости, ибо в математике существуют формальные правила, позволяющие переносить все нужные математические факты из одной системы отсчета в другую. Механическая суть задачи при этом не страдает. С подобной проблемой мы уже сталкивались при изучении плоской задачи теории упругости в декартовых и полярных координатах. Здесь, как и там, мы воспользуемся формальным аппаратом перехода от одной системы отсчета к другой. В соответствии с этим формализмом, чтобы перенести результаты теории изгиба прямоугольных пластин в полярные координаты
и вытекающими из нее дифференциальными соотношениями
Рассматривая теперь прогиб
Повторяя подобные выкладки, получим
Отсюда видно, что уравнение Софи Жермен в полярных координатах имеет вид
где под
В полярных координатах роль напряжений
аналогичными (2.2)-(2.4). Выразим величины (6.7) через функцию прогиба, ограничиваясь случаем действия на пластину лишь поперечных нагрузок. Для этого, вообще говоря, естественно воспользоваться связью полярных компонент напряжений с декартовыми, выражениями последних через функцию прогиба и правилами перехода от производных
Подставляя сюда выражения (2.2)-(2.4), с учетом (6.4) найдем
Аналогичным образом можно выразить через
Граничные условия на краю
если этот край защемлен (рис. 6.З а),
если он шарнирно оперт (рис. 6.3 6), и
если этот край свободен (рис. 6.З в); В случае края
где Приведенные выше зависимости позволяют ставить и решать различные задачи изгиба круглых пластин и пластин в форме кольцевого сектора. Далее мы ограничимся изучением одного важного частного случая - осе симметричного изгиба круглых пластин.
6.2. Осесимметричный изгиб круглых пластин. Осесимметричный изгиб реализуется в круглых пластинах, когда граничные условия и действующая на пластину внешняя нагрузка не зависят от полярного угла. В таком случае естественно считать, что все величины, описывающие напряженно-деформированное состояние пластины, также не зависят от полярного угла  . Все это приводит к существенному упрощению выражений предыдущего пункта. . Все это приводит к существенному упрощению выражений предыдущего пункта.
Так уравнение Софи Жермен (6.5) принимает вид
или
и имеет общее решение
где последним слагаемым представлено частное решение
которое, в случае постоянной нагрузки
Зависимости (6.16), (6.17) получаются путем последовательного выполнения операций интегрирования в уравнении (6.15). Постоянные интегрирования
Упрощенные условия вида (6.10)-(6.12) можно теперь записать так
на кромке
на кромке Если область, занимаемая срединной плоскостью пластины, — круг (
Отсюда приходим к выводу, что здесь следует принять
так что
С другой стороны, в рассматриваемом случае w* = 0 и следовательно
Сравнивая формулы (6.24), (6.25), находим
Таким образом, эта константа отлична от нуля лишь тогда, когда в центре пластины приложена сосредоточенная поперечная сила. В этом общем случае
Оставшиеся две постоянные
|

 и
и 

 как сложную функцию
как сложную функцию  , находим
, находим
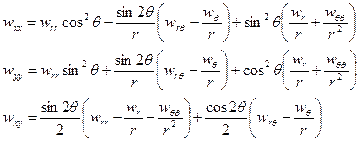

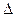 теперь понимается оператор Лапласа в полярных координатах:
теперь понимается оператор Лапласа в полярных координатах:
 ,
, 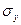 ,
,  ,
,  ,
, 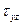 играют напряжения
играют напряжения  ,
,  ,
, 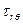 ,
, 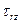 ,
, 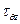 . Вместо декартовых обобщенных внутренних сил
. Вместо декартовых обобщенных внутренних сил  ,
,  ,
, 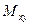 ,
,  ,
, 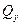 вводятся внутренние силы
вводятся внутренние силы  ,
,  ,
,  ,
,  ,
,  (см. рис. 6.1), связанные о полярными компонентами напряжений зависимостями
(см. рис. 6.1), связанные о полярными компонентами напряжений зависимостями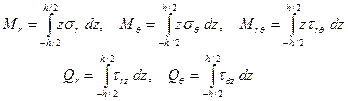
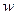 по
по  и
и 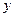 к производным по
к производным по  и
и 
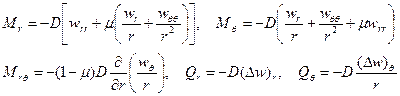
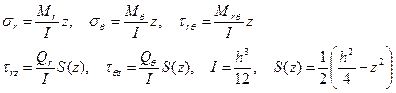
 записываются так:
записываются так: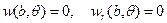


 ,
,  — заданные условием задачи величины.
— заданные условием задачи величины. условия (6.10)-(6.12) принимают соответственно вид
условия (6.10)-(6.12) принимают соответственно вид
 — заданные величины.
— заданные величины.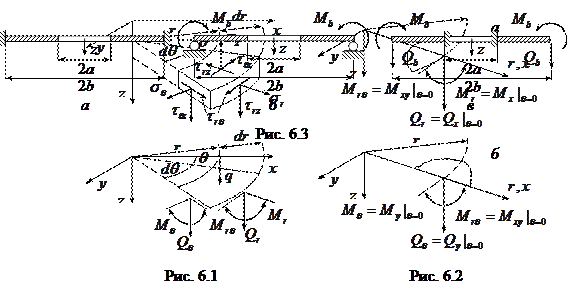



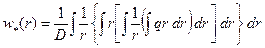 ,
,
 , определяется по формуле
, определяется по формуле
 следует находить из краевых условий вида (6.10)-(6.12) после упрощения их для осесимметричного случая. На каждом крае пластины
следует находить из краевых условий вида (6.10)-(6.12) после упрощения их для осесимметричного случая. На каждом крае пластины 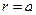 и
и  ) имеется ровно два условия. Конкретное начертание их мы дадим чуть позже. А сейчас заметим, что формулы (6.8) в рассматриваемом варианте изгиба принимают вид
) имеется ровно два условия. Конкретное начертание их мы дадим чуть позже. А сейчас заметим, что формулы (6.8) в рассматриваемом варианте изгиба принимают вид

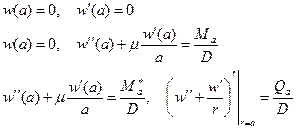
 ,
,  ,
, 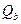 — заданные постоянные величины.
— заданные постоянные величины. ), то вместо условий вида (6.21) необходимо потребовать ограниченность прогиба в точке
), то вместо условий вида (6.21) необходимо потребовать ограниченность прогиба в точке  :
:
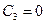 и общее решение задачи писать в виде
и общее решение задачи писать в виде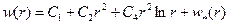
 Выясним смысл постоянной
Выясним смысл постоянной 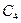 . Предположим, что к пластине приложена только сосредоточенная поперечная сила
. Предположим, что к пластине приложена только сосредоточенная поперечная сила 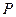 в центре
в центре 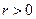 и рассмотрим его равновесие в отношении проекций на ось
и рассмотрим его равновесие в отношении проекций на ось 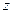 всех действующих на него сил (рис. 6.4). Имеем
всех действующих на него сил (рис. 6.4). Имеем

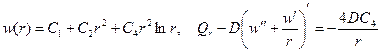

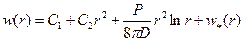
 найдутся из граничных условий на кромке
найдутся из граничных условий на кромке 


