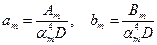Методы решения задач изгиба прямоугольных пластин
Выше было показано, что исследование поперечного изгиба пластины свелось к бигармонической краевой задаче относительно функции прогиба. Эта математическая проблема изучена достаточно хорошо, а для ее решения предложены как аналитические, так и численные методы. Мы ограничимся рассмотрением методов двойных и одинарных тригонометрических радов, позволяющих находить точные решения в виде ряда Фурье, и приближенных аналитических методов Ритца-Тимошенко и Бубнова Галеркина.
Решению подлежит краевая задача
Предположим, что искомая функция
с неизвестными, подлежащими определению, коэффициентами Представление (5.12) находится в полном согласии со всеми краевыми условиями (5.2), (5.3). Следовательно, коэффициенты
с коэффициентами
Чтобы показать это, достаточно умножить формальное разложение (5.5) на
Подставляя ряды (5.4), (5.5) в уравнение (5.1), придем к равенству
Функциональный ряд обращается тождественно (при любых
Таким образом, искомое решение задачи имеет вид
и, как видно, свелось к вычислению интегралов вида (5.6). Впервые оно получено Навье и потому носит его имя. По прогибу пластины (5.9) можно теперь найти любые интересующие нас величины. Например, для изгибающих моментов
Сравнивая эти ряды с (5.9), убеждаемся в их худшей сходимости. Так что для достижения одной и той же точности вычислений в формулах (5.10) по сравнению с выражением (5.9) нужно удержать большее число членов ряда. В заключение еще раз подчеркнем, что построенное решение справедливо лишь для шарнирно опертых по всем кромкам прямоугольных пластин. Требование выполнения условий Дирихле для функции поперечной нагрузки практически не столь обременительно.
Имеем следующую краевую задачу
Методом двойных тригонометрических рядов воспользоваться здесь непосредственным образом уже нельзя. Будем считать, что искомая функция
коэффициенты которого, зависящие от координаты
и будут выполняться при любых
В соответствии с принятым соглашением функция
с коэффициентами
Подставляя (5.15), (5.17) в (5.12), приходим к равенству
Отсюда следует, что
Общее решение этого дифференциального уравнения имеет вид
Здесь
то последнее можно найти подбором в том же линейном виде
Действительно, подставляя два последних выражения в (5.19), получим
и, следовательно,
На определении постоянных Метод одинарных тригонометрических рядов имеет более широкую область использования по сравнению с предыдущим методом. Для его применения достаточно наличия двух каких-либо шарнирно опертых противоположных кромок. Ясно, что его можно применить и тогда, когда все кромки пластины шарнирно оперты. Проиллюстрируем этот метод именно на таком примере.
|

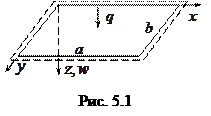 5.1. Метод двойных тригонометрических рядов (решение Навье). Рассмотрим шарнирно опертую по всему контуру прямоугольную пластину под действием поперечной нагрузки
5.1. Метод двойных тригонометрических рядов (решение Навье). Рассмотрим шарнирно опертую по всему контуру прямоугольную пластину под действием поперечной нагрузки  (рис. 5.1). Будем считать, что функция
(рис. 5.1). Будем считать, что функция 


 также удовлетворяет условиям Дирихле по
также удовлетворяет условиям Дирихле по  и
и  , и поэтому может быть представлена в виде двойного тригонометрического ряда
, и поэтому может быть представлена в виде двойного тригонометрического ряда
 . Предположение о свойствах функции
. Предположение о свойствах функции  должны отыскиваться из требования выполнения разрешающего уравнения задачи (5.1). По предположению функция поперечной нагрузки представима в виде двойного ряда Фурье
должны отыскиваться из требования выполнения разрешающего уравнения задачи (5.1). По предположению функция поперечной нагрузки представима в виде двойного ряда Фурье
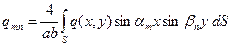
 (
( ), а затем проинтегрировать его по области
), а затем проинтегрировать его по области  с учетом очевидного условия ортогональности
с учетом очевидного условия ортогональности
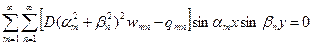
 и
и 


 и
и  имеют место формулы (см. (2.2))
имеют место формулы (см. (2.2))
 5.2. Метод одинарных тригонометрических рядов (решение Леви). Предположим теперь, что прямоугольная пластина шарнирно оперта, по крайней мере, по двум каким-либо противоположным кромкам. Пусть, например, — это кромки
5.2. Метод одинарных тригонометрических рядов (решение Леви). Предположим теперь, что прямоугольная пластина шарнирно оперта, по крайней мере, по двум каким-либо противоположным кромкам. Пусть, например, — это кромки  (рис. 5.2). На двух других кромках допустимы любые граничные условия. Для определенности примем, что кромка
(рис. 5.2). На двух других кромках допустимы любые граничные условия. Для определенности примем, что кромка 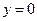 защемлена, а кромка
защемлена, а кромка  шарнирно оперта. Нагрузка
шарнирно оперта. Нагрузка 




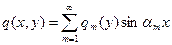




 — частное решение неоднородного уравнения (5.20), а
— частное решение неоднородного уравнения (5.20), а  — постоянные интегрирования, для нахождения которых в нашем распоряжении имеется необходимое количество условий (5.16). В частности, если
— постоянные интегрирования, для нахождения которых в нашем распоряжении имеется необходимое количество условий (5.16). В частности, если  — линейная подфункция
— линейная подфункция