Метод Ритца-Тимошенко.
Пример 1. Проиллюстрируем применение метода Ритца-Тимошенко на примере той же шарнирно опертой по всему контуру прямоугольной пластины. Следуя процедуре этого метода, зададим искомую функцию
где
обеспечивают выполнение геометрических граничных условий
Система функций
Дальнейшая схема реализации метода Ритца-Тимошенко
требует подстановки (5.24) в (5.27), интегрирования по области
Отсюда и находятся искомые величины
Это позволяет избежать стандартное возведение в квадрат ряда типа (5.24) и, тем самым, сократить объем выкладок. Имея в виду, что
с учетом условий ортогональности (см. (5.7), (5.25))
из уравнений (5.28) находим
Здесь
Итак, искомое приближенное решение имеет вид
и, как и следовало ожидать, в пределе при Пример 2. Проиллюстрируем метод на примере пластины, свободной от нагрузки по всему контуру поперечного сечения. Функционал полной энергии такой пластины представим в форме (4.5)
где искомая функция прогиба ищется в виде ряда
Здесь система функций Если это возможно, то функция двух переменных задается в виде комбинации функций одной переменной, так
При выбранных функциях
Система (5.33) всегда относительно констант линейна
где при всех четырех опертых кромках
Здесь
где символом (k) обозначены функция, ее первая и вторая производные k=0,1,2.
|

 приближенно в виде частичной суммы ряда
приближенно в виде частичной суммы ряда
 — искомые числовые параметры, а аппроксимирующие функции
— искомые числовые параметры, а аппроксимирующие функции  , выбранные в форме
, выбранные в форме

 (
(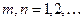 ) — линейно независимая, полная и ортогональная в области
) — линейно независимая, полная и ортогональная в области  . В силу (5.26) для полной энергии изгиба пластины справедливо упрощенное выражение (4.6):
. В силу (5.26) для полной энергии изгиба пластины справедливо упрощенное выражение (4.6):

 :
:





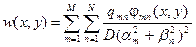
 переходит в точное решение (5.9).
переходит в точное решение (5.9).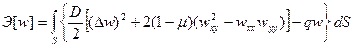 , (4.5)
, (4.5)
 (5.32)
(5.32)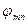 выбрана так, чтобы смещения были возможными, то есть линейно независимыми, непрерывными, полными и удовлетворяющими на контуре пластины всем геометрическим граничным условиям. При этом функции могут удовлетворять и статическим граничным условиям, но это не обязательно.
выбрана так, чтобы смещения были возможными, то есть линейно независимыми, непрерывными, полными и удовлетворяющими на контуре пластины всем геометрическим граничным условиям. При этом функции могут удовлетворять и статическим граничным условиям, но это не обязательно.
 , подставив (5.32) в (4.5) и произведя интегрирование, мы получим функцию, зависящую только от констант
, подставив (5.32) в (4.5) и произведя интегрирование, мы получим функцию, зависящую только от констант  . Условие ее минимума
. Условие ее минимума (5.33)
(5.33) ,
,




