Метод Бубнова-Галеркина.
При иллюстрации и этого метода мы вновь ограничимся рассмотренным выше случаем шарнирно опертой по всему контуру прямоугольной пластины, т.е. вернемся к Примеру 1. По-прежнему зададим искомую функцию приближенно в виде (5.24), (5.25), обеспечивающем выполнение всех краевых условий задачи (5.2), (5.3). Для нахождения искомых числовых параметров
Подставляя сюда выражение (5.24), приходим к равенству
из которого с учетом условия ортогональности (5.29) и формулы (5.31) находим
Как и следовало ожидать, мы получили тот же результат, что и в методе Ритца-Тимошенко (см. (5.31)).
Перейдем к Примеру 2. Решение задачи, как и в предыдущем случае, ищется в форме ряда (5.32) с теми же требованиями к аппроксимирующим функциям. Различие состоит в следующем. По методу Ритца функционал полной энергии минимизируется впрямую, то есть ищется такая комбинация констант, которая обеспечивает этому функционалу минимум на ограниченном множестве функций По методу Бубнова-Галеркина условие минимума этого функционала записывается по правилам вариационного исчисления
где под контурными интегралами стоит разность между внутренними силовыми факторами на контуре пластины
и соответствующими им внешними факторами, Точное решение задачи дает экстремаль, удовлетворяющая уравнению Эйлера и естественным граничным условиям на контуре пластины
Если выбором функций
В силу произвольности и независимости вариаций при константах
Выражение (5.34), расписанное с помощью (5.32)
где
Отметим два факта. При выборе одних и тех же функций коэффициенты системы (5.35), несмотря на разницу в форме представления, по существу всегда одинаковы. Если функции выбраны так, что статические граничные условия выполнены, то контурные интегралы в (5.36) исчезают.
|

 в методе Бубнова-Галеркина служит система
в методе Бубнова-Галеркина служит система
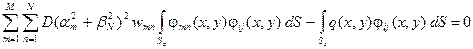

 .
. (5.33)
(5.33)

 , если таковые приложены по контуру пластины.
, если таковые приложены по контуру пластины.


 равенство нулю возможно только при обнулении констант при каждом члене ряда.
равенство нулю возможно только при обнулении констант при каждом члене ряда. (5.34)
(5.34) (5.35)
(5.35)
 (i=1,2,…,n j=1,2,…,n) (5.36)
(i=1,2,…,n j=1,2,…,n) (5.36)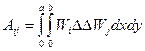 (i=1,2,…,n j=1,2,…,n)
(i=1,2,…,n j=1,2,…,n)


