Обобщенные силы и перемещения
В предыдущем параграфе мы выяснили характер зависимости по Приведение напряжений к обобщенным силам имеет смысл для нормальных сечений пластины, образуемых при рассечении ее цилиндрической поверхностью (в частности, плоскостью), перпендикулярной срединной плоскости. Условимся, при этом, линию пересечения такой цилиндрической поверхности и срединной плоскости называть контуром нормального сечения пластины. Напомним, что всякая система плоских параллельных сил статически эквивалентна силе и моменту, причем величина последнего зависит от выбранной точки приведения сил. Воспользуемся этим фактом и путем интегрирования по толщине перейдем в нормальных сечениях пластины от напряжений к статически эквивалентным им погонным интегральным силовым факторам. При этом, конечно, надо фиксировать плоскость, к которой мы будем приводить напряжения. В качестве таковой удобно (хотя и не обязательно) принять срединную плоскость пластины. Рассмотрим плоские нормальные сечения пластины, параллельные координатным плоскостям
Они отличны от нуля в плоском напряженном состоянии. Проинтегрируем те же выражения по толщине пластины, умножив их предварительно на координату
и крутящему моменту
Интегрируя, далее, по толщине пластины выражения (1.12), (1.13), получим погонные перерезывающие силы
Выражения (2.2), (2.3) относятся к физическим соотношениям теории изгиба пластин, чего нельзя сказать о выражениях (2.4), порожденные через поперечные касательные напряжения статическими уравнениями. Не представляет теперь труда выразить напряжения через введенные выше обобщенные силы. Сравнивая (1.9), (1.12), (1.13) с (2.2)-(2.4), находим
Таким образом, при анализе напряженного состояния пластины вместо напряжений (2.5) можно изучать связанные с ними прямыми зависимостями обобщенные силы (2.2)-(2.4). Они являются, по существу, равнодействующими соответствующих напряжений, собранных в нормальных координатных сечениях с толщины пластины и снесенных статически эквивалентным образом на ее срединную плоскость. Это иллюстрируется на рис. 2.1, где вверху изображен соответствующий фрагмент пластины, на нормальных сечениях которой показаны действующих там напряжений, а внизу — фрагмент срединной плоскости с прямыми контурами координатных нормальных сечений, на которых показаны положительно направленные обобщенные силы. Уравнения равновесия пластины в обобщенных силах можно получить из рассмотрения равновесия бесконечно малого элемента срединной плоскости пластины. Такой элемент изображен на рис. 2.2, где показаны и действующие на него силы и моменты. Символами
Сразу же отметим, что три из шести уравнений равновесия такого элемента, а именно, сумма всех сил на оси  и и  и моментов вокруг оси и моментов вокруг оси  , дают тривиальные тождества , дают тривиальные тождества  . Они приобретают не тривиальный вид в плоском напряженном состоянии. . Они приобретают не тривиальный вид в плоском напряженном состоянии.
Приравнивая нулю сумму проекций на ось
Поделим полученное уравнение на
Расписывая подобным образом уравнения моментов действующих на элемент срединной плоскости пластины сил относительно его правой и ближней горизонтальной кромок, параллельных соответственно осям
которые, как не трудно убедиться, после подстановки в них зависимостей (2.2)-(2.4) обращаются в тождества вида Обратимся теперь к выяснению смысла обобщенных перемещений. Рассмотрим сначала нормальное сечение пластины
Будем считать заданным прогибы
Итак, в теории пластин роль обобщенных играют смещения точек срединной плоскости и угол поворота нормального сечения вокруг касательной его контура.
Разобьем контур сечения
(участок Теперь мы вправе сказать, что в нормальном сечении
Совершенно аналогично показывается, что в сечении
которым отвечают соответственно обобщенные смещения В силу (2.3), (2.4)
|

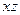 и
и  . На них возникают напряжения (1.9), (1.12), (1.13). Интегрируя по толщине пластины выражения (1.9), приходим к нулевым погонным тангенциальным усилиям
. На них возникают напряжения (1.9), (1.12), (1.13). Интегрируя по толщине пластины выражения (1.9), приходим к нулевым погонным тангенциальным усилиям




 и
и  обозначены приращения величин за счет изменения координат
обозначены приращения величин за счет изменения координат  и
и 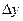 соответственно.
соответственно.

 , сокращая предварительно подобные члены, и перейдем к пределу при
, сокращая предварительно подобные члены, и перейдем к пределу при  и
и  (бесконечно малый элемент срединной поверхности стягиваем в точку). Вспоминая определение частной производной, приходим к уравнению
(бесконечно малый элемент срединной поверхности стягиваем в точку). Вспоминая определение частной производной, приходим к уравнению

 , параллельное плоскости
, параллельное плоскости 
 точек контура сечения. В таком случае можно найти и величину
точек контура сечения. В таком случае можно найти и величину  .Для полного описания смещений всех точек сечения достаточно задать еще одну величину —
.Для полного описания смещений всех точек сечения достаточно задать еще одну величину —  . Аналогичные рассуждения показывают, что смещения точек нормального сечения
. Аналогичные рассуждения показывают, что смещения точек нормального сечения  полностью характеризуются двумя величинами
полностью характеризуются двумя величинами  и
и  :
:
 Сопоставим теперь введенные выше обобщенные силы и перемещения. Если, например, рассматривать нормальное сечение
Сопоставим теперь введенные выше обобщенные силы и перемещения. Если, например, рассматривать нормальное сечение  , то первое, что бросается в глаза, так это количественное несовпадение обобщенных смещений и обобщенных сил. Обобщенных смещений — два (
, то первое, что бросается в глаза, так это количественное несовпадение обобщенных смещений и обобщенных сил. Обобщенных смещений — два ( ,
,  ), а обобщенных сил — три (
), а обобщенных сил — три ( ,
,  ,
,  ). Обобщенным силам
). Обобщенным силам  , которая, как было показано выше, не является независимым обобщенным смещением. Поэтому напрашивается вывод о том, что и крутящий момент
, которая, как было показано выше, не является независимым обобщенным смещением. Поэтому напрашивается вывод о том, что и крутящий момент  определяется обычным образом:
определяется обычным образом:
 и обобщенная перерезывающая сила
и обобщенная перерезывающая сила
 возникают изгибающий момент
возникают изгибающий момент  и обобщенная перерезывающая сила
и обобщенная перерезывающая сила ,
,
 и
и  .
.



