Неоднозначность нахождения первообразной
Дифференцирование функции – однозначная операция, т.е. если функция имеет производную, то только одну. Это утверждение непосредственно следует из определений предела и производной: если функция имеет предел, то только один. Обратная операция – отыскание первой производной – не однозначна. Так, функции Теорема. Если
Пусть Неопределённый интеграл и его свойства Первообразную можно находить не только по данной её производной, но и по её дифференциалу. Определение. Совокупность всех первообразных Таким образом, если
где С – любое действительное число. Наличие постоянной С делает задачу нахождения функции по её производной не вполне определённой; отсюда происходит и само название «неопределённый интеграл». Пользуясь определением неопределённого интеграла, можно записать:
Поэтому, чтобы найти неопределённый интеграл от заданной функции, нужно найти какую-нибудь одну её первообразную и прибавить к ней произвольную постоянную С. Чтобы проверить, правильно ли найден неопределённый интеграл, необходимо продифференцировать полученную функцию; если при этом получается подынтегральное выражение, то интеграл найден верно. Например, Основные свойства неопределённого интеграла 1. Производная неопределённого интеграла равна подынтегральной функции, т.е.
2. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла, т.е.
где m – постоянная величина, не равная нулю. 3. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е.
4. Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е.
5. Неопределённый интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С, т.е.
|

 ,
,  ,
,  ,
,  , где С – любое постоянное действительное число, являются первообразными функции
, где С – любое постоянное действительное число, являются первообразными функции  , поскольку все эти функции имеют 4 x 3.
, поскольку все эти функции имеют 4 x 3.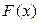 является первообразной функции
является первообразной функции  на некотором промежутке, то множество всех первообразных этой функции имеет вид
на некотором промежутке, то множество всех первообразных этой функции имеет вид  , где С – любое действительное число.
, где С – любое действительное число. Доказательство. Пусть
Доказательство. Пусть  . Тогда
. Тогда 
 . Покажем теперь, что все первообразные функции
. Покажем теперь, что все первообразные функции  – другая первообразная функции
– другая первообразная функции  . Тогда
. Тогда 
 при всех x из рассматриваемого промежутка. Следовательно,
при всех x из рассматриваемого промежутка. Следовательно,  , что и требовалось установить. Отсюда следует, что задача нахождения первообразной имеет бесконечное множество решений. Геометрически выражение
, что и требовалось установить. Отсюда следует, что задача нахождения первообразной имеет бесконечное множество решений. Геометрически выражение  представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси 0Y.
представляет собой семейство кривых, получаемых из любой из них параллельным переносом вдоль оси 0Y.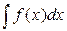 , где
, где  – подынтегральное выражение, x – переменная интегрирования.
– подынтегральное выражение, x – переменная интегрирования.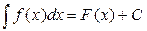 ,
, и т.д.
и т.д. . Сделаем проверку:
. Сделаем проверку:  или
или  . Следовательно, интеграл найден верно.
. Следовательно, интеграл найден верно. .
. ,
,
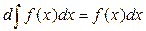
 или
или 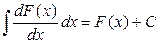 .
.


