Нахождение первообразной по начальным или граничным условиям
При интегрировании функции получается совокупность её первообразных. Для выделения из всей совокупности конкретной первообразной задают дополнительные данные, которые называют начальными условиями (если аргументом является параметр времени t) или граничными условиями (если аргументом являются координаты x, y, z). При решении таких задач используют следующий алгоритм: 1. Находят неопределённый интеграл от заданной функции. 2. Вычисляют величину постоянной С, подставляя начальные условия в совокупность первообразных для заданной функции. 3. Находят искомую первообразную, заменяя в совокупности первообразных постоянную интегрирования её вычисленным значением. Пример. Найти функцию, производная которой равна Решение. 1. Из условия следует, что искомая функция является первообразной функции
2. Из полученного выражения 3. Итак, искомая функция имеет вид Пример. Найти функцию, обращающуюся в нуль при Решение. 1. Все первообразные функции имеют вид: 2. При 3. Искомая функция имеет вид: Составление уравнения движения точки по заданному уравнению скорости или ускорения её движения Из кинематики точки известно, что уравнение движения точки при векторном способе задания её движения имеет вид: При координатном способе задания движения точки уравнения движения имеют вид (для декартовой системы координат):
Здесь x, y, z – координаты точки, t – время (уравнения движения определяют зависимость координат точки от времени). По определению проекции скорости точки есть первые производные от соответствующих координат: Пример. Точка движется прямолинейно и ось 0Х декартовой системы координат совпадает с траекторией точки. Проекция ускорения на ось 0Х изменяется со временем по закону Решение. 1. Имеем 2. Используя начальные условия:
3. Следовательно: 4. Имеем 5. Используя начальные условия: Отсюда: 6. Следовательно:
|

 , если известно, что при
, если известно, что при  функция принимает значение, равное 25.
функция принимает значение, равное 25. .
. , определяющего все первообразные функции
, определяющего все первообразные функции  , откуда С =19.
, откуда С =19. .
. , если производная этой функции имеет вид
, если производная этой функции имеет вид  .
. .
. .
. , где
, где  – радиус-вектор точки, t – время (уравнение движения определяет зависимость радиуса-вектора точки от времени). По определению скорость точки есть первая производная от радиуса-вектора точки по времени:
– радиус-вектор точки, t – время (уравнение движения определяет зависимость радиуса-вектора точки от времени). По определению скорость точки есть первая производная от радиуса-вектора точки по времени:  . По определению ускорение точки есть первая производная от скорости точки по времени или вторая производная от радиуса-вектора точки по времени:
. По определению ускорение точки есть первая производная от скорости точки по времени или вторая производная от радиуса-вектора точки по времени:  .
.
 . По определению проекции ускорения точки есть первые производные от соответствующих проекций скоростей точки по времени или вторые производные от соответствующих координат точки по времени:
. По определению проекции ускорения точки есть первые производные от соответствующих проекций скоростей точки по времени или вторые производные от соответствующих координат точки по времени:  .
. . Найти уравнение движения
. Найти уравнение движения 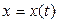 и зависимость
и зависимость  . В момент времени
. В момент времени  проекция скорости
проекция скорости  , координата
, координата  .
. .
. . Отсюда:
. Отсюда: .
.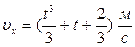 .
.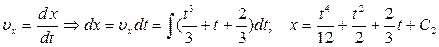 .
. .
. .
. .
.


