Способ интегрирования по частям
При интегрировании функций, содержащих произведения, логарифмы и обратные тригонометрические функции, бывает удобно воспользоваться способом интегрирования по частям. Выведем формулу интегрирования по частям: дифференциал от произведения равен Нахождение интеграла При практическом использовании формулы интегрирования по частям данное интегральное выражение представляют в виде произведения двух сомножителей, которые обозначают u и dυ;. Множитель u стараются выбирать так, чтобы du было проще, чем u. Рассмотрим частные примеры интегрирования по частям. Пример 1. Вычислить РЕШЕНИЕ: Интеграл содержит произведение двух функций x и
Приняв x=u, получили Если же в данном интеграле сделать другую замену: Пример 2. Вычислить РЕШЕНИЕ:
Пример 3. Вычислить РЕШЕНИЕ: Имеем:
Для нахождения полученного в правой части равенства интеграла снова интегрируем по частям (см. решение примера 1):
В результате получаем окончательный ответ:
Пример 4. Вычислить РЕШЕНИЕ:
Определённый интеграл Определение. Если F(x)+C – первообразная функция для f(x), то приращение F(b) – F(a) первообразных функций при изменении аргумента x от x=a до x=b называется определённым интегралом и обозначается символом Функция f(x) предполагается непрерывной в промежутке изменения аргумента x от a до b. Для вычисления определённого интеграла 1) неопределённый интеграл 2) значение интеграла F(x)+C при x=b, C=0, т.е. вычисляют F(b); 3) значение интеграла F(x)+C при x=a, C=0, т.е. вычисляют F(a); 4) разность F(b) – F(a). Процесс вычисления виден из формулы
Данное равенство называется формулой Ньютона-Лейбница.
Так как приращение F(b) – F(a) равно некоторому числу, то определённый интеграл есть число (в отличие от неопределённого интеграла, который есть совокупность функций). Геометрический смысл определённого интеграла заключается, очевидно, в том, что Основные свойства определённых интегралов При рассмотрении будем предполагать, что функция f(x) непрерывна на отрезке [ a, b ]. 1. При перестановке пределов интегрирования знак интеграла меняется на противоположный:
2. Постоянный множитель можно вынести за знак определённого интеграла:
где k – постоянная величина. 3. Определённый интеграл от алгебраической суммы функций равен алгебраической сумме определённых интегралов от этих функций:
|

 ; в результате интегрирования имеем
; в результате интегрирования имеем 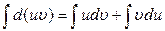 или
или  . Откуда:
. Откуда:  .
. сводится к нахождению интеграла
сводится к нахождению интеграла  , который может оказаться или проще данного, или даже известным.
, который может оказаться или проще данного, или даже известным. .
. . Способ подстановки не даёт возможности найти этот интеграл. Обозначим x=u,
. Способ подстановки не даёт возможности найти этот интеграл. Обозначим x=u,  ; тогда dx = du;
; тогда dx = du;  . Применим формулу интегрирования по частям:
. Применим формулу интегрирования по частям: .
. и интеграл
и интеграл 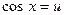 ,
,  , то можно убедиться, что полученный интеграл окажется сложнее исходного, т.е. замена окажется неудачной. Умение определить целесообразность той или иной замены приходит с приобретением навыка.
, то можно убедиться, что полученный интеграл окажется сложнее исходного, т.е. замена окажется неудачной. Умение определить целесообразность той или иной замены приходит с приобретением навыка. .
. .
. . Иногда формулу интегрирования по частям приходится применить дважды.
. Иногда формулу интегрирования по частям приходится применить дважды.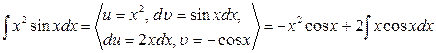 .
. .
. .
. .
.
 .
. , т.е.
, т.е.  , где a – нижний предел, b – верхний предел определённого интеграла.
, где a – нижний предел, b – верхний предел определённого интеграла. ;
; .
. Под F(x) в формуле понимают простейшую из первообразных функций, у которой C=0.
Под F(x) в формуле понимают простейшую из первообразных функций, у которой C=0. .
. ,
,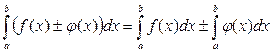 .
.


