Предельное распределение
Результаты серии измерений одной величины можно наглядно представить, построив диаграмму, которая показала бы, как часто получены те или иные значения. Такая диаграмма называется гистограммой. Пусть, например, выполняется подсчет частиц, которые регистрируются счетчиком за одну минуту. Выполнено десять измерений и получены следующие результаты: 56, 59, 54, 58, 56, 57, 56, 58, 57, 57. Эти результаты удобно записать в виде следующей таблицы, располагая их по мере возрастания значения.
Полученные результаты позволяют вычислить среднее значение регистрируемых за одну минуту частиц:
где N – число измерений. Величину, определяющую долю от полного числа измерений, в которой реализуется результат xк принято называть частотой.
При этом среднее значение можно определить по формуле
Частоты Fk характеризует распределение результатов измерений в виде гистограмм, на которых по вертикальной оси откладывают значения Fk, а по горизонтальной - x k.
Рис. 2 Если сложить частоты всех возможных значений x k, то в результате получается единица
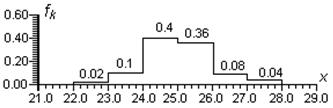
Это условие называют условием нормировки. Гистограмма, представленная на Рис.2 определяет распределение дискретной величины. Вместе с этим, часто встречаются физические величины, имеющие непрерывный диапазон возможных значений. Например, при измерении расстояния между линзой и изображением предмета, могут быть получены следующие результаты (в сантиметрах): 26,4; 23,9; 25,1; 24,6; 22,7; 23,8; 25,2; 23,7; 25,3; 25,4. Если по полученным результатам построить гистограмму, подобную предыдущей, то она будет содержать десять черточек одинаковой высоты и являться малоинформативной. Поэтому диапазон возможных значений разбивают на интервалы и подсчитывают, какое количество измерений попадает в каждый интервал. Выбирая интервал в размере Δ k = 1,0 см, можно построить следующую гистограмму для непрерывной функции:
Рис. 3 Причем для непрерывной величины площадь f k Δ k к-го прямоугольника (на Рис.3 он заштрихован) имеет такой же смысл, что и высота к-той черточки F k в случае гистограммы для дискретной величины (см. Рис.2). При увеличении числа измерений N можно уменьшить ширину интервала Δk. Так на Рис.4а представлена гистограмма в случае ста измерений того же расстояния x при Δk = 1,0, а на Рис.4б – в случае тысячи измерений при Δk = 0,5.
а)
б) Рис. 4 Гистограммы на Рис. 4 иллюстрируют важное свойство большинства измерений: с ростом числа измерений их распределение стремится к некоторой определенной непрерывной кривой – предельному распределению, которая соответствует гистограмме при N ® ¥ и Δk ® 0. При наличии только случайных погрешностей предельное распределение представляет собой симметричную колоколообразную кривую, показанную на Рис.4б. Конечно, предельное распределение – теоретическая идеализация, которую никогда нельзя точно получить в эксперименте. Предельное распределение определяет функцию, называемую плотностью распределения, которую обозначим f(x). Если известна f(x), можно разделить весь интервал значений x на малые интервалы от xk до xk + Δ xk. Тогда доля значений, попавшая в каждый такой интервал, будет Fk = f (xk)Δ xk и формула (3.1.3), определяющая среднее значение величины, в пределе, когда все интервалы стремятся к нулю примет вид
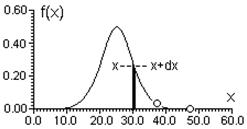
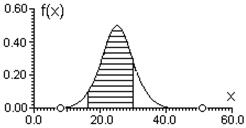
Доля измерений (при N ® ¥), которая попадает в любой бесконечно малый интервал от x до x + dx, будет равна площади f(x) dx заштрихованного участка на Рис.5а. В случае интервала конечной ширины. например от x1 до x2, доля от полного числа измерений, попадающих в данный интервал равна площади под кривой между x = x1 и x = x2 (Рис.5б). Она определяется путем интегрирования: доля измерений в интервале от x1 до x2 равна
а) б) Рис. 5 Сказанное можно выразить другим очень полезным способом:
Отсюда можно сделать важное заключение: если бы было известно предельное распределение f(x) для результатов измерений данной величины x, то можно найти вероятность получения результата в любом заданном интервале x1 £ x £ x2. Предельное распределение f(x) должно удовлетворять условию нормировки (аналогично (3.1.4) для дискретной функции): которое означает, что при единичном измерении вероятность получения результата в пределах от -¥ до +¥ равна единице. Наиболее употребительной мерой, характеризующей рассеяние случайной величины, является дисперсия, обозначаемая D x и определяемая по формуле
По аналогии с (3.1.5), когда N ® ¥ дисперсия определяется через функцию распределения
Квадратный корень из дисперсии называется среднеквадратичным или стандартным отклонением и обозначается sx
|

 , (3.1.1)
, (3.1.1)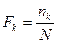 (3.1.2)
(3.1.2)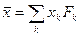 (3.1.3)
(3.1.3)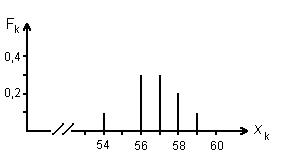
 (3.1.4)
(3.1.4)

 (3.1.5)
(3.1.5) .
.
 (3.1.6)
(3.1.6)
 , (3.1.7)
, (3.1.7)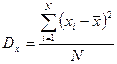 (3.1.8)
(3.1.8) (3.1.9)
(3.1.9) (3.1.10)
(3.1.10)


