Ранее было сказано, что среди погрешностей измерений могут встречаться промахи – погрешности, существенно превышающие ожидаемые значения при данных условиях эксперимента. Поэтому возникает естественный вопрос – какие погрешности следует считать промахами с целью исключения в дальнейшем соответствующих им результатов измерения? Эта оценка осуществляется на основе критерия Шовене.
Пусть проделано N измерений некой величины x и получены следующие результаты:  . На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить
. На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить  и
и  . Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют
. Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют
 – (3.5.1)
– (3.5.1)
– число выборочных стандартных отклонений, на которое  отличается от
отличается от  . По таблице 2 Приложения можно найти вероятность Р (вне
. По таблице 2 Приложения можно найти вероятность Р (вне  ) того, что нормальное измерение будет отличаться от
) того, что нормальное измерение будет отличаться от  на
на  или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне
или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне  ) на полное число измерений N, чтобы получить
) на полное число измерений N, чтобы получить
n(хуже, чем  ) = N·P(вне
) = N·P(вне  ), (3.5.2)
), (3.5.2)
которое определяет число ожидаемых измерений, которые дают столь же плохие результаты, что и  . Если n меньше 0,5, то
. Если n меньше 0,5, то  отбрасывается. В этом состоит критерий Шовене. После отбрасывания результата, не удовлетворяющего критерию Шовене, надо пересчитать
отбрасывается. В этом состоит критерий Шовене. После отбрасывания результата, не удовлетворяющего критерию Шовене, надо пересчитать  и
и  по оставшимся данным. При n большем 0,5 следует всё оставить без измерения.
по оставшимся данным. При n большем 0,5 следует всё оставить без измерения.
Рассмотрим пример: произведено шесть измерений некоторой величины и получены следующие результаты:
3,8; 3,5; 3,9; 3,9; 3,4; 1,8.
Среди этих результатов подозрительным является 1,8. Поэтому с учётом шести измерений рассчитываем  =3,4 и
=3,4 и  =0,8. Значение 1,8 отличается от
=0,8. Значение 1,8 отличается от  на
на 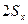 . Согласно таблицы 1 Приложения:
. Согласно таблицы 1 Приложения:
Р(вне 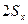 )=1 – Р(в пределах
)=1 – Р(в пределах 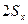 ) = 0,05.
) = 0,05.
То есть из двадцати возможных результатов измерений приблизительно только один должен также сильно отличаться от  , как число 1,8. в случае проведённых шести измерений ожидаемое число таких результатов n=0,05, 6=0,3. Поскольку n<0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений
, как число 1,8. в случае проведённых шести измерений ожидаемое число таких результатов n=0,05, 6=0,3. Поскольку n<0,5, то, согласно критерию Шовене, подозрительный результат x=1,8 должен быть исключён, а для оставшихся значений  =3,7,
=3,7,  =0,23.
=0,23.

 . На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить
. На основании этих значений по формулам (3.4.1) и (3.4.2) можно вычислить  и
и  . Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют
. Если имеется подозрительный результат, погрешность которого, возможно, является промахом, то для него вычисляют – (3.5.1)
– (3.5.1) отличается от
отличается от  . По таблице 2 Приложения можно найти вероятность Р (вне
. По таблице 2 Приложения можно найти вероятность Р (вне  ) того, что нормальное измерение будет отличаться от
) того, что нормальное измерение будет отличаться от  или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне
или более выборочных стандартных отклонений. Наконец, следует умножить полученную вероятность Р(вне  ) на полное число измерений N, чтобы получить
) на полное число измерений N, чтобы получить ) = N·P(вне
) = N·P(вне  и
и  по оставшимся данным. При n большем 0,5 следует всё оставить без измерения.
по оставшимся данным. При n большем 0,5 следует всё оставить без измерения. =3,4 и
=3,4 и 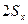 . Согласно таблицы 1 Приложения:
. Согласно таблицы 1 Приложения:


