Функция Гаусса
В математике функция, график которой имеет форму колоколообразной кривой, называется функцией нормального распределения или функцией Гаусса. Она имеет следующий вид:
Функция Гаусса описывает предельное распределение результатов измерений величины x, истинное значение которой равно X. Причем при измерении величины x оказываются только случайные ошибки. Принято считать, что результаты измерений распределены нормально, если их предельное распределение описывается функцией Гаусса. В формуле (3.2.1) величина σ является фиксированным параметром, который определяет ширину гауссовой кривой в точках перегиба. Малые значения σ приводят к распределению типа острого пика, которое соответствует более точным измерениям, в то время как большие значения σ дают широкое распределение, соответствующее измерениям с малой точностью. На Рис.6 представлены два примера графиков функций Гаусса с различными значениями величин Х и σ;. Видно, что величина σ в знаменателе предэкспоненциального множителя формулы (3.2.1) обеспечивает для более узкого распределения (малые σ;) большую высоту в точке x = X. Это обусловлено тем, что функция Гаусса нормирована, то есть для нее выполнено условие (3.1.6). Поэтому площадь под кривой, выражающей на графике функцию Гаусса, при любых значениях σ; и X должна равняться единице.
Рис. 6 Функция Гаусса отражает следующие предположения, лежащие в основе теории случайных погрешностей и подтверждаемые опытом: 1. Погрешности результатов наблюдений принимают непрерывный ряд значений. 2. При большом числе наблюдений одинаково часто встречаются погрешности одного значения, но разных знаков. 3. Частота появления погрешностей уменьшается с возрастанием их значений. В случае распределения Гаусса среднее значение величины X определяется, согласно (3.1.5), по формуле:
Интеграл можно вычислить, что приведёт к следующему результату:
Отсюда можно сделать вывод: если результаты измерений распределены в соответствии с функцией Гаусса, то в случае бесконечно большого числа измерений среднее значение Для дисперсии (3.1.9) в случае распределения Гаусса получим
Результат интегрирования:
Поскольку, согласно (3.1.10), корень из дисперсии есть стандартное отклонение, то
Следовательно: параметр
|

 (3.2.1)
(3.2.1)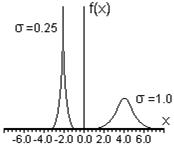
 . (3.2.2)
. (3.2.2) (3.2.3)
(3.2.3) будет равно истинному значению
будет равно истинному значению  , которое соответствует центру функции Гаусса.
, которое соответствует центру функции Гаусса. (3.2.4)
(3.2.4) (3.2.5)
(3.2.5) . (3.2.6)
. (3.2.6) ширины функции Гаусса есть стандартное отклонение, которое мы получили бы в случае бесконечно большего числа измерений.
ширины функции Гаусса есть стандартное отклонение, которое мы получили бы в случае бесконечно большего числа измерений.


