Предположим, что результаты измерений величины x распределены нормально около истинного значения X с шириной  . Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение
. Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение  . Нас интересует, как распределены полученные значения
. Нас интересует, как распределены полученные значения  .
.
Величина  есть простая функция измеренных значений
есть простая функция измеренных значений 
 . (3.7.1)
. (3.7.1)
Поэтому можно найти распределение  с помощью расчёта ошибок для косвенных измерений.
с помощью расчёта ошибок для косвенных измерений.
Поскольку каждое из измеренных значений  распределено нормально, то очевидно, что и
распределено нормально, то очевидно, что и  также имеют нормальное распределение. Так как истинным значением для
также имеют нормальное распределение. Так как истинным значением для  является X, то и истинным значением
является X, то и истинным значением  является также X. Следовательно, полученные значения
является также X. Следовательно, полученные значения  распределены нормально около истинного значения X. Ширину этого распределения можно найти по формуле:
распределены нормально около истинного значения X. Ширину этого распределения можно найти по формуле:
 . (3.7.2)
. (3.7.2)
Но:
 , (3.7.3)
, (3.7.3)
а из (3.5.1) следует:
 . (3.7.4)
. (3.7.4)
Следовательно, вместо (3.5.2) получаем:
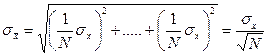 (3.7.5)
(3.7.5)
Эту величину называют стандартным отклонением среднего. Видно, что при  значение
значение 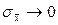 .
.
Вывод: значения  распределены нормально с центром, равным истинному значению и с шириной
распределены нормально с центром, равным истинному значению и с шириной  ; другими словами, если найдено однажды
; другими словами, если найдено однажды  , то вероятность попадания этого значения в интервал
, то вероятность попадания этого значения в интервал  равна 68%.
равна 68%.
Для оценки стандартного отклонения среднего, которую обозначим  , используют формулу
, используют формулу
 . (3.7.6)
. (3.7.6)
Величину  называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измерений N растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:
называют выборочным стандартным отклонением среднего. Видно, что при увеличении числа измерений N растёт точность измерения. Стандартное отклонение среднего при косвенных измерениях может быть определено по формуле:
 . (3.7.7)
. (3.7.7)
Пример: определим выражение для стандартного отклонения величины q, которая связана с величинами x, y, z, определяемыми прямыми измерениями, следующим соотношением:
 , (3.7.8)
, (3.7.8)
где  – точные числа.
– точные числа.
Для частных производных получаем:
 . (3.7.9)
. (3.7.9)
После подстановки (3.7.9) в (3.7.7) имеем:
 . (3.7.10)
. (3.7.10)

 . Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение
. Необходимо узнать, какова надёжность среднего значения для N измерений. Для ответа на этот вопрос представим себе, что N измерений повторяются много раз, причём в каждом случае определяется среднее значение  . Нас интересует, как распределены полученные значения
. Нас интересует, как распределены полученные значения 
 . (3.7.1)
. (3.7.1) распределено нормально, то очевидно, что и
распределено нормально, то очевидно, что и  . (3.7.2)
. (3.7.2) , (3.7.3)
, (3.7.3) . (3.7.4)
. (3.7.4)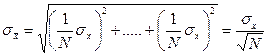 (3.7.5)
(3.7.5) значение
значение 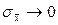 .
. ; другими словами, если найдено однажды
; другими словами, если найдено однажды  равна 68%.
равна 68%. , используют формулу
, используют формулу . (3.7.6)
. (3.7.6) . (3.7.7)
. (3.7.7) , (3.7.8)
, (3.7.8) – точные числа.
– точные числа. . (3.7.9)
. (3.7.9) . (3.7.10)
. (3.7.10)


