Вероятность попадания результата однократного измерения в заданный интервал
Для распределения Гаусса вероятность попадания результата измерения в определённый интервал при однократном измерении, согласно (3.1.6), определяется по формуле: P (в пределах где t – положительное число, После подстановки Р (в пределах Этот интеграл называют функцией ошибок (или нормальным интегралом ошибок), который обозначается erf(t). Его значение при произвольном t аналитически не вычисляется и определяется только численными методами. В таблице 2 Приложения приведены значения функции ошибок для различных значений t. Вероятность может быть определена как в виде десятичной дроби, так и в процентах. На рис.7 изображена зависимость функции ошибок от параметра t в процентах.
Рис.7 Из таблицы 2 Приложения или рис.7 видно, например, что вероятность попадания в интервал полуширина которого соответствует одному стандартному отклонению Используя таблицу 2 Приложения легко определить вероятность попадания результата единичного измерения в интервал с произвольными границами x1 и x2, то есть когда x1 и x2 отличаются от X на одинаковое значение Вероятность того, что ожидаемый результат однократного измерения окажется вне определённого интервала можно определить по формуле: Р (вне Поэтому, например, вероятность попадания результата единичного измерения за пределы интервала с полушириной
|

 ) =
) = 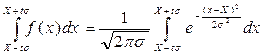 , (3.3.1)
, (3.3.1) ,
,  получим:
получим: ) =
) =  (3.3.2)
(3.3.2)
 равна 68%, 2
равна 68%, 2 


