Если a, b, c принадлежат интервалу, на котором функция f(x) непрерывна, то
Вычисление определённых интегралов Пример 1. Найти РЕШЕНИЕ:
Пример 2. Найти РЕШЕНИЕ:
Пример 3. Найти РЕШЕНИЕ: Для вычисления определённого интеграла с помощью подстановки поступают так же, как и вычислении неопределённого интеграла этим способом. Однако в случае определённого интеграла имеется особенность, на которую следует обратить внимание. Метод подстановки заключается в том, что для приведения заданного неопределённого интеграла к табличному выражают аргумент через новую переменную, а затем находят неопределённый интеграл и полученный результат снова выражают через первоначальную переменную. В случае же определённого интеграла нет необходимости возвращаться к первоначальной переменной, однако нужно помнить, что, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования. Воспользуемся подстановкой
Пример 4. Найти РЕШЕНИЕ:
Пример 5. Найти РЕШЕНИЕ:
Пример 6. Найти РЕШЕНИЕ:
Пример 7. Найти РЕШЕНИЕ:
Применение определённого интеграла к решению физических задач Схема решения задач на приложения определённого интеграла С помощью определённого интеграла можно решать различные задачи физики, которые трудно или невозможно решить методами элементарной математики. Понятие определённого интеграла применяется при решении задач на вычисление работы переменной силы, давления жидкости на вертикальную поверхность, пути, пройденного точкой, движущейся с переменной скоростью, и ряд других. Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через х, а промежуток её изменения – через [ a, b ]. Отрезок [ a, b ] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка. На каждой такой части задачу решат по формулам для постоянных величин. Далее составляют сумму (интегральную сумму), выражающую приближённое значение искомой величины. Переходя к пределу при n→∞;, находят искомую величину I в виде интеграла
|

 .
.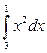 .
. .
. .
.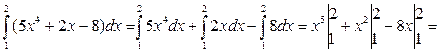
 .
. .
. , откуда
, откуда  . Затем найдём новые пределы интегрирования: подставляя в равенство
. Затем найдём новые пределы интегрирования: подставляя в равенство  и
и  , соответственно получим
, соответственно получим  и
и  . Запись решения выглядит так:
. Запись решения выглядит так:
 .
.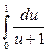 .
. .
. .
. .
. .
.
 .
. .
.
 .
. , где f(x) – данная по условиям задачи функция (сила, скорость и т.д.).
, где f(x) – данная по условиям задачи функция (сила, скорость и т.д.).


