Основные формулы интегрированияИз определения интеграла следует, что для того чтобы проинтегрировать функцию, нужно найти её первообразную. Для ряда функций это легко сделать, используя соответствующую формулу дифференцирования. Формула интегрирования получаются обращением соответствующих формул дифференцирования. Основные интегралы выпишем в таблицу.
Интегралы, приведённые в этой таблице, называются табличными интегралами. Примеры: применяя табличные интегралы удаётся вычислить следующие интегралы. ИНТЕГРИРОВАНИЕ ПО ФОРМУЛЕ 1:
ИНТЕГРИРОВАНИЕ ПО ФОРМУЛЕ 2:
ИНТЕГРИРОВАНИЕ ПО ФОРМУЛАМ 3 И 4:
ИНТЕГРИРОВАНИЕ ПО ФОРМУЛАМ 5 И 6:
Применяя формулу
Применяя формулы
ИНТЕГРИРОВАНИЕ ПО ФОРМУЛАМ 7 И 8:
Применяя формулы
Проинтегрируем, применяя различные приёмы преобразования подынтегрального выражения:
Может показаться, что для одного и того же интеграла получено три различных ответа. Однако это не так. Можно убедиться в том, что любые из ответов отличаются друг от друг только на постоянную величину. ИНТЕГРИРОВАНИЕ ПО ФОРМУЛАМ 9 И 10:
Приложения неопределённого интеграла
|
при n ≠ – 1
;
;
;
.
;
;
.
;
.
;
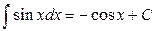
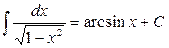
вычисляется интеграл
;
вычисляется интеграл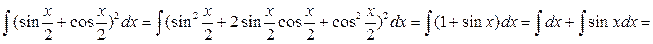
.
;
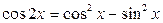вычисляется интеграл
;
;
;
.
;
.
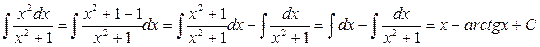