Цикл Карно
В состоянии 1 газ приводится в контакт с холодильником и отдает ему теплоту (Q х).
Итак, цикл Карно состоит из следующих термодинамических процессов: изотермического 3®4; адиабатического 4®1; изотермического 1®2 и адиабатного 2®3. При количественном анализе цикла Карно необходимо обращаться к формулам и определениям, рассмотренным нами ранее в разделе 1. Так, для изотермического процесса 3®4:
Q н = L 3®4 = (М /μ) RТ н.ln(V 4/ V 3), (1.32)
а для изотермического процесса 1®2:
Q х = L 1®2 = (М /μ) RТ хln(V 2/ V 1). (1.33)
Полезная работа цикла определяется алгебраической суммой: L0 = L 3®4 + L 1®2. С другой стороны, полезная работа совершается за счет алгебраической суммы теплот L 0 = Q н + Q х. Таким образом, энергетический баланс запишется в виде:
Q н + Q х = L 3®4 + L 1®2 = (М /μ) R (Т н ln(V 4/ V 3) + Т х ln(V 2/ V 1)). (1.34)
Используя уравнения адиабаты, для точек 4 и 1: р 4 V 4 k = р 1 V 1 k и для точек 2, 3: р 3 V 3 k = р 2 V 2 k, применяя так же уравнения изотерм: р 3 V 3 = р 4 V 4 (3®4) и р 1 V 1 = р 2 V 2 (1®2), найдем соотношение: V 4/ V 3 = V 1/ V 2. Последнее позволит упростить уравнение (1.35):
Q н + Q х = (М /μ) R (Т н - Т х)ln(V 4/ V 3). (1.35)
Последняя формула позволит определить термический коэффициент полезного действия цикла Карно (h). Согласно определению, он равен отношению полезно затраченной теплоты ко всей исходной теплоте процесса:
h = (Q н + Q х)/ Q н.
Подставляя в определительное уравнение для h выражения из формул (1.36) и (1.33) найдем:
|
Цикл Карно начинается с изотермического процесса 3®4 в котором, получивший от нагревателя теплоту (Q н) газ расширяется, производя работу. Затем, контакт с нагревателем прерывается, но газ продолжает расширяться 4®1 в адиабатических условиях.
При этом, вследствие инерционности двигателя и присоединенных движущихся деталей поршень начинает сжатие газа 1®2. Процесс сжатия продолжается и дальше 2®3, но уже адиабатно, без теплового контакта с холодильником. Затем цикл повторяется (рисунок 1.5).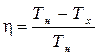
(1.36)
