Цикл двигателя внутреннего сгорания с подводом теплоты
при постоянном объеме (цикл Отто) Идеальный теоретический цикл Отто (рисунок 1.6) характеризует работу 4-хтактного двигателя, в котором газотопливная смесь наполняет цилиндр при ходе поршня к нижней мертвой точке - НМТ (четвертый такт), а затем при обратном ходе поршня к верхней мертвой точке - ВМТ (первый такт) смесь сжимается и возле ВМТ срабатывает система зажигания. Топливо воспламеняется и отдает свое тепло Q н практически при постоянном объеме (состояние 2 на рисунке 1.6). Затем следует второй такт, в котором происходит адиабатное расширение газов. В конце этого процесса (состояние 3) открывается выпускной клапан и газы теряют тепло (Q х) в окружающую среду. Последний процесс происходит тоже при почти постоянном объеме. Третий такт практически завершает удаление отработавших газов в атмосферу. Таким образом, идеальный термодинамический цикл Отто состоит (см. рисунок 2.2) из адиабатного процесса сжатия: 1®2, изохорного ввода теплоты Q н: 1®3, адиабатного расширения газов: 3®4 и изохорного отвода теплоты Q х: 4®1. При количественном анализе циклов двигателей внутреннего сгорания выявляют следующие характеристики:
e = V 1/ V 2 = (V 2 + V h)/ V 2, (1.37) где V h - рабочий объем цилиндра - объем, описываемый поршнем при его перемещении от верхней мертвой точки (ВМТ) до нижней мертвой тоски (НМТ):
V h = V 1 – V 2, (1.38)
Степень повышения давления:
l= р 3/ р 2 . (1.39)
Термический к.п.д.: h = L 0 / Q н. В рассматриваемом идеальном цикле теплота теряется лишь при передаче холодильнику (процесс 4®1), поэтому можно записать:
h = (Q н + Q х)/ Q н. (1.40)
Величины теплот выразим через характеристики изохорных процессов 2®3 и 4®1:
Q н = M сv (Т 3 - Т 2) и Q х = M сv (Т 1 - Т 4). (1.41)
После подстановки и преобразований получим:
На основании рассмотренных ранее термодинамических соотношений можно получить: для адиабаты 1®2 Т 2 = Т 1e k -1; для изохоры 2®3 Т 3 = Т 2 .l = Т 1.l.e k -1 ; для адиабаты 3®4 Т 4 = Т 3 . e1- k = Т 1 . l. После подстановки и преобразований получаем:
Среднее давление цикла. Определяется согласно усредняющей формуле:
р 0= L 0/ Vh. (1.44)
Работа в данном цикле совершается лишь в адиабатических процессах:1®2- сжатие (работа L 1®2) и 3®4 - расширение (работа L 3®4 ). Поэтому L 0= L 3®4 + L 1®2. Величины работ выразятся уравнением:
После подстановок и преобразований получим следующее расчетное уравнение
Цикл двигателя внутреннего сгорания с сообщением теплоты
Далее второй такт осуществляется адиабатически (3®4) и заканчивается как и в цикле Отто изохорическим (4®1) выведением теплоты (Q х) холодильнику (окружающая среда). После полного выброса отработавших газов (третий такт) цилиндр заполняется воздухом (четвертый такт).
Имеется и характерный только для этого цикла параметр - степень предварительного расширения:
r = V 3/ V 2. (1.47) При количественном рассмотрении цикла найдем вначале выражение для к.п.д. Определительная формула: h = (Q н + Q х)/ Q н. Величину Q н найдем, рассматривая изобарныий процесс 2®3, а величину Q х по формулам изохорного процесса:
Q н = M ср (Т 3 - Т 2); Q х = Mсv (Т 1 - Т 4). (1.48)
Подставляя найденные величины в уравнение для к.п.д., а также заменяя значения температур Т 3, Т 2, Т 4, выраженные через Т 1 после записи соотношений для частных термодинамических процессов Т 2 = Т 1e k -1 (из уравнений адиабаты 1®2); Т 3 = Т 2r = Т 1 e k -1 r (из уравнений изобары 2®3); Т 4 = Т 3 e1- k = Т 1 r k, получим в итоге:
Среднее давление цикла найдем, определив все работы цикла: работу изобарического расширения L 2®3 = (М/ m) R (Т 3 - Т 2); работу адиабатического расширения L 3®4 = (М /μ)(k - 1)-1 R (Т 3 - Т 4); работу адиабатического сжатия L 1®2 = (М /μ)(k - 1)-1 R (Т 2 - Т 1). Полная работа цикла определится алгебраической суммой L 0 = L 2®3 + L 3®4 + L 2®1. После подстановки в эту сумму слагаемых и преобразований получим вначале:
Затем, определяем среднее давление цикла (р 0 = L0 / Vh). Для этого выражаем величину Vh через V 1: Vh = V 1 (1 - 1/e), а затем вводим р 1 = (М /μ) RТ 1 V 1-1. В итоге получим выражение:
Цикл двигателя с сообщением теплоты при постоянных
Смешанный цикл (рисунок 1.8) состоит из адиабатического процесса сжатия 1®2, изохорического процесса 2®3, изобарического процесса Смешанный тепловой цикл, как и прежде рассмотренные циклы двигателей внутреннего сгорания характеризуется во многом уже известными параметрами и характеристиками. Вывод формул для количественного выражения параметров цикла аналогичен рассмотренным в теоретических разделах методических указаний.
степень сжатия:
e = V 1/ V 2;
степень предварительного расширения:
r = V 4/ V 3 = V 4/ V 2;
степень повышения давления:
l = р 3/ р 2 = р 4/ р2.
Термический к.п.д. цикла Тринклера:
Теплоты цикла:
Q н = Q 1 + Q 2 = Mсv (Т 3 - Т 2) + Mср (Т 4 - Т 3) , Qх = Mсv (Т 1 - Т 5). (1.53)
Работа цикла:
Среднее давление цикла:
где р 0 = L 0/ Vh, Vh = V 1 - V 2.
|
Степень сжатия двигателя:
. (1.42)
. (1.43)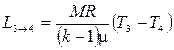
; 
. (1.45)
. (1.46)
В данном цикле поршень, совершая первый такт, сжимает воздух до достаточно высоких давлений (30 - 40 . 105 Па) Растет температура, применяются также более высокие степени сжатия (14-22). При приближении поршня к ВМТ в верхний объем цилиндра над поршнем впрыскивается под значительным давлением топливо. Физические показатели процесса в этот момент таковы, что топливо самовоспламеняется. Так как топливо постепенно поступает через форсунку, то резкого повышения давления не наблюдается и поэтому можно считать, что тепло (Q н) поступает в процесс при постоянстве давления. Таким образом, в начале второго такта выполняется изобарический процесс (2®3, рисунок 1.7).
Равновесный теоретический цикл Дизеля составляется (рисунок 2.3) из последовательности процессов: адиабата 1®2 - сжатие, изобара 2®3 - расширение и подвод тепла, адиабата 3®4 - расширение и изохора 4®1 - отвод тепла. Также как и цикл Отто, данный цикл характеризуют: степенью сжатия e = V 1/ V 2, термическим к.п.д. (h), средним давление цикла р 0 = L 0/ Vh.
. (1.49)
. (1.50)
. (1.51)
Цикл характеризуется следующими, уже известными соотношениями:
. (1.52)
. (1.54)
, (1.55)
