ПРИМЕНЕНИЕ t-КРИТЕРИЯДля вычисления уровня статистической достоверности различия между двумя средними[2], в случае, если эти значения измерены в интервальной шкале или шкале отношений, используется t -критерий. Существует три типа t -критерия: для одной выборки, для независимых и зависимых выборок.
Критерий t-Стьюдента для одной выборки
Критерий t-Стьюдента для независимых выборок (примерный)
Критерий t-Стьюдента для независимых выборок (точный) для выборок разных объемов
Критерий t-Стьюдента для зависимых выборок
Чтобы определить величину t, потребуются формулы для вычисления SS – сумм квадратов, δ2 – дисперсии, SD – стандартного отклонения и df – степеней свободы (см. выше):
´ Задача 2.20 (вариант с одной выборкой).Выделяются ли ученики с высоким осенним СБ из всей массы учеников? Вначале вычисляем среднее арифметическое показателя Х5, А = 4,418 После этого формируем матрицу для учеников с высоким осенним СБ и вычисляем среднее арифметическое M, отклонения D, квадраты отклонений D2, сумму квадратов отклонений SS, дисперсию δ2, стандартное отклонение SD и ошибку среднего m. Затем определяем t -критерий Стьюдента и сравниваем его с табличным.
Обращаясь к табл. П 3.4 и имея df = 8, а уровень значимости p = 0,05, мы получаем критическое значение 2,306, которое выше рассчитанного нами. Вывод. Средние баллытех, кто занимается лучше, статистически значимо не отличаются от СБ всей выборки (от ожидаемого среднего значения). ´ Задача 2.21 (вариант с независимыми выборками).Имеют ли учащиеся с высоким уровнем знаний более высокие осенние СБ, чем учащиеся, которые занимаются хуже? Для решения задачи необходимо сформировать матрицы для учеников с высоким осенним СБ и для учеников с низким осенним СБ, затем вычислить для каждой из выборок среднее арифметическое M, отклонения D, квадраты отклонений D2, сумму квадратов отклонений SS, дисперсию δ2, стандартное отклонение SD и ошибку среднего m. После чего определить t -крите-рий Стьюдента и сравнить его с табличным. Матрицу для учеников с высоким осенним СБ мы уже обработали в примере выше, осталось повторить аналогичные вычисления для матрицы для учеников с низким осенним СБ.
По формуле для вычисления примерного критерия t -Стьюдента для независимых выборок получаем:
По формуле для вычисления точного критерия t -Стьюдента для независимых выборок разных объемов получаем
Обращаясь к табл. П 3.4 и имея df = 15, а уровень значимости р = 0,05, мы выбираем критическое значение 2,131. Полученная нами величина t = 2,317превышает 2,131 и может считаться статистически значимой на уровне 0,05. Поэтому мы заключаем, что средние баллы тех, кто занимается лучше, статистически значимо отличаются от СБ тех, кто занимается хуже.
Обращаясь к табл. П 3.4 и имея df = 8, а уровень значимости 0,05, выбираем критическое значение 2,306. Подсчитанная нами величина t = 1,047 не превышает 2,306 и не может считаться статистически значимой на уровне 0,05. Вывод. Между весенними и осенними СБ отсутствуют статистически значимые различия. ´ Задача 2.23 (дополнительный пример). Какая методика эффективнее для развития параметра А (кистевая динамометрия) путем вычисления уровня статистической достоверности различия между двумя средними по t -критерию Стьюдента на уровне значимости p < 0,05. Перед проведением эксперимента были сформированы две группы – контрольная и экспериментальная – по 12 испытуемых, которые прошли тест по параметру А.
КГ 68 65 71 69 64 62 62 67 59 61 65 64 ЭГ 67 68 72 65 67 61 64 61 62 69 60 65
По соответствующим формулам вычисляем степень свободы df и t -критерий для независимых выборок. Значения заносим в соответствующие ячейки таблицы:
Выполняем расчеты, как это показано в таблице ниже (например, в программе MS Excel). Обращаясь к табл. П 3.4 и имея df = 22 для независимых выборок, а уровень значимости 0,05, выбираем критическое значение 2,074. Рассчитанное в примере t11-21= 0,227 меньше табличного, поэтому: тесты по параметру А, выполненные перед проведением эксперимента, показали, что статистически достоверных различий между группами КГ и ЭГ по параметру А нет. Вывод. В таких условиях МОЖНО начинать проводить эксперимент.
В течение двух недель испытуемые КГ тренировались по методике F, а экспериментальной – по методике G. Затем было проведено повторное тестирование параметра А:
КГ 72 68 71 69 67 64 63 67 61 62 64 65 ЭГ 69 70 74 72 69 65 68 70 64 72 68 68
По соответствующим формулам вычисляем степень свободы df и t -критерий для зависимых выборок. Подсчитанные нами величины t указывают, что после 2 недель тренировок в обеих группах произошли статистически достоверные изменения. Статистически достоверно (t12-22= 2,304) стали различаться и данные КГ и ЭГ, а показатель экспериментальной группы t21-22= 2,828больше показателя контрольной группы t11-12= 2,259. Обращаясь к табл. П 3.4 и имея df = 22 для независимых и df = 22 для зависимых выборок, а уровень значимости 0,05, выбираем критические значения – соответственно 2,074 для независимых и 2,201 для зависимых выборок. Вывод. Методика G экспериментальной группы оказалась более эффективной, чем методика F, которая применялась для развития параметра А в контрольной группе.
|
, 
, где ошибка среднего 
.
, 
.
.
, 
.
, 
, 
.
.
.
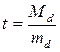´ Задача 2.22 (вариант с зависимыми выборками).Отличается ли весенний СБ от осеннего СБ у учащихся с высоким уровнем знаний?
.
