Дисперсионный анализ

Дисперсионный анализ (ANOVA) является одним из наиболее полезных и универсальных статистических методов, применяемых в психологии в настоящее время. Его можно использовать в экспериментах с межгрупповыми (bg) и внутригрупповыми (wg) планами и в экспериментах, которые имеют несколько уровней категориальной независимой переменной, но только одну количественную зависимую переменную. Дисперсионный анализ основан на F -распределении. Основные формулы для подсчета F приведены в таблице.

Формулы	Сумма квадратов	Число степеней свободы	Средние квадраты
Общая Total		dftotal = N – 1
Межгрупповая Between Group		dfbg = k – 1
Внутригрупповая Within Group		dfwg= = dftotal – dfbg = = N – k
Коэффициент детерминации		F-отношение Фишера

´ Задача 2.24. Зависит ли количество отработанных часов Х 7 от уровня удовлетворенности учебой Х 8? Для проведения этого анализа нам потребуется данные Х 7 всех испытуемых (n =17) расположить в 3 группы (k =3), каждая из которых будет соответствовать определенному уровню удовлетворенности учебой X 8.

Вначале вычисляем общее средние арифметические M_total = 24 и групповые M_group1 = 25, M_group2 = 24, M_group3. = 22.

Затем вычисляем отклонения D от M_total и квадраты отклонений D².

Вычисляем общую сумму квадратов отклонений SS_total = 1776.

По формуле вычисляем межгрупповую (Between Group) сумму квадратов отклонений

.

Вычисляем внутригрупповую (Within Group) сумму квадратов отклонений

.

Определяем степени свободы: df_bg = k – 1 = 3 – 1 = 2; df_total = N – 1 = 16;

df_wg = df_total – df_bg = 16 – 2 = N – k = 17 – 3 = 14.

Теперь вычисляем межгрупповой (Between Group) средний квадрат:

.

И внутригрупповой (Within Group) средний квадрат: .

X 8	X 7	D	D2	Mgroup
		–14
		–14
		-9
		–14
		–12
		–4
		–4
		–14
	Mtotal = 24		SStotal = 1776
			SSbg = 23
			SSwg = 1753
			R2 = 0,01
			dfbg = 2
			dfwg = 14
			MSbg = 11
			MSwg = 125
			F = 0,091
	p = 0,05		FT = 3,316

 

Наконец, вычисляем критерий Фишера

.

После того как рассчитана величина F, необходимо обратиться к табл. П 3.5, в которой величины даны парами, где верхнее число соответствует критическому значению на уровне 0,05, а нижнее – критическому значению на уровне 0,01. Столбцы расположены в соответствии со степенями свободы между группами (df_bg), а строки – в соответствии со степенями свободы внутри групп (df_wg). Чтобы получить критическое значение для нашего анализа, двигайтесь вниз по столбцу для df_bg = 2, пока не достигнете строки, соответствующей df_wg = 14. Перед нами две величины, 3,74 и 6,51, Поскольку полученная нами величина F (0,091) не превышает 3,74, делаем вывод, что наши результаты статистически незначимы, т. е. между количеством отработанных часов и уровнем удовлетворенности учебой нет никакой связи.
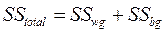
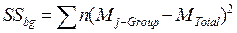
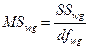
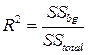