Вероятностные распределения
Вероятность события определяется как возможность того, что это событие произойдёт. Например, в прогнозе погоды может сообщаться: «Вероятность того, что сегодня будет дождь 40%, а вероятность того, что дождя не будет – 60%». Если перечисляются все возможные события (исходы, результаты) и если каждому из них приписывается определенный уровень вероятности, то такой список называется вероятностным распределением (распределением вероятностей), или просто распределением. Заметьте, что сумма вероятностей должна составлять 1,0, или 100%. Вероятности можно также приписывать и возможным значениям доходности (или денежным потокам) от инвестиций. Рассмотрим возможную доходность, которую вы можете получить в следующем году при вложении 10 тыс. ден.ед. в акции либо компании «М», либо компании «А». Компания «М» производит маршрутизаторы и другое электронное оборудование для быстро развивающейся индустрии передачи данных. Компании приходится работать в условиях жесткой конкуренции, её новые товары могут быть, а могут и не быть конкурентоспособными на рынке, и поэтому её будущие объёмы продаж и прибыли точно предсказать чрезвычайно трудно. В свою очередь компания «А» предоставляет услуги водопровода и канализации. Поскольку вход других фирм на этот рынок обычно крайне затруднен из-за эффекта масштаба, она может не бояться появления конкурентов и считать свои объёмы производства относительно стабильными. Такой же будет и её прибыль – из-за государственного регулирования тарифов локальных естественных монополий. Вероятностные распределения доходности акций обеих компаний представлены в таблице 5.1. Предполагается, что существует 30%-ная вероятность наступления рыночного бума, что будет означать высокий спрос на их продукцию и относительно высокие прибыли обеих компаний. В этом случае компании будут выплачивать высокие дивиденды, а их акции – приносить капитальную прибыль. Существует 40%-ная вероятность среднего спроса и умеренных прибылей, а также 30%-ная вероятность ограниченного спроса, что приведёт к невысоким прибылям и дивидендам, а также к отсутствию капитальной прибыли или даже к убыткам. Тем не менее, доходность акции компании «М» может варьироваться в значительно более широком диапазоне, чем «А». Существует значительная вероятность того, что цена акций «М» значительно, на 70% снизится, в то время как возникновение убытков от вложения акций «А» исключается. Таблица 5.1 Вероятностные распределения доходности акций компаний «М» и «А».
25. Ожидаемый уровень доходности Если мы умножим каждое из возможных значений некоторого показателя на вероятность того, что оно будет достигнуто, и затем сложим эти произведения, как сделано в таблице 5.2, мы получим ожидаемое, среднее значение этого показателя, или просто его среднее (обозначается k). Показанные в таблице 5.2 средние доходности по акциям компании «М» и «А» составляют по15%, а таблица такого рода называется матрицей выигрышей. Вычисление предполагаемой нормы прибыли можно также выразить с помощью формулы, которая демонстрирует те же вычисления, что и таблица матрицы выигрышей: (формула 5.1) Ожидаемая доходность актива равна (формула 5.1): где Можно изобразить графически.
Измерение автономного риска: среднеквадратическое отклонение Чтобы быть полезной для практического использования, любая мера риска должна иметь точное определение – нам необходима мера «сжатости» распределения вероятности. Одной из таких мер является среднеквадратическое (стандартное) отклонение (СКО) – обозначается Среднеквадратическое отклонение = Таким образом, среднеквадратическое (стандартное) отклонение доходности – это в определенном смысле средневзвешенное отклонение от её ожидаемого значения, и оно показывает, насколько выше или ниже ожидаемой окажется вероятная фактическая доходность. Эмпирическое Здесь Эмпирическое значение Измерение автономного риска: коэффициент вариации Если необходимо сделать выбор между двумя инвестициями, имеющими одинаковую среднюю доходность, но различные среднеквадратические отклонения, большинство людей сделает выбор в пользу того варианта, при котором отклонение меньше и соответственно риск ниже. Аналогично при выборе между двумя инвестициями с одинаковым риском (среднеквадратическим отклонением), но разной доходностью инвесторы обычно предпочитают ту, у которой средняя доходность будет выше. Но как сделать выбор между двумя вариантами вложения капитала, если один из них предполагает и большую доходность, и больший риск одновременно? Для ответа на этот вопрос мы часто используем особую меру риска — коэффициент вариации, который вычисляется как среднеквадратическое отклонение, деленное на среднюю ожидаемую доходность (формула 5.5):
|

 (5.1)
(5.1) - это один из возможных исходов (i – его номер),
- это один из возможных исходов (i – его номер),  - вероятность этого исхода, а n – общее число возможных исходов. Таким образом,
- вероятность этого исхода, а n – общее число возможных исходов. Таким образом, 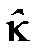 - это средневзвешенное значение доходности, при этом весом каждого отдельного её значения
- это средневзвешенное значение доходности, при этом весом каждого отдельного её значения  Чем более «сжатым» будет график распределения вероятности, тем ближе окажется фактическая доходность к ожидаемой и, следовательно, тем меньше вероятность, что действительная прибыль окажется значительно ниже предполагаемой. Таким образом, чем более «сжато» распределение вероятности, тем ниже риск, задаваемый акции. Поскольку у компании «А» распределение вероятности весьма сжато, её фактическая доходность с большей вероятностью будет близка к ожидаемым 15%, чем доходность компании «М».
Чем более «сжатым» будет график распределения вероятности, тем ближе окажется фактическая доходность к ожидаемой и, следовательно, тем меньше вероятность, что действительная прибыль окажется значительно ниже предполагаемой. Таким образом, чем более «сжато» распределение вероятности, тем ниже риск, задаваемый акции. Поскольку у компании «А» распределение вероятности весьма сжато, её фактическая доходность с большей вероятностью будет близка к ожидаемым 15%, чем доходность компании «М». . Чем меньше квадратическое отклонение, тем более распределение вероятности «сжато» и соответственно тем ниже риск акций.
. Чем меньше квадратическое отклонение, тем более распределение вероятности «сжато» и соответственно тем ниже риск акций.
 = S =
= S = 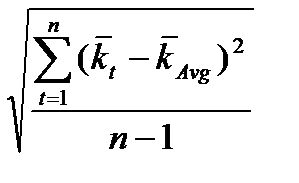
 означает фактическую доходность в году t, а
означает фактическую доходность в году t, а 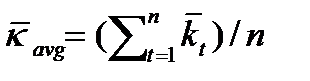 - среднегодовая доходность за n последних лет.
- среднегодовая доходность за n последних лет. часто используется для прогнозирования будущего
часто используется для прогнозирования будущего  .
. Коэффициент вариации отражает риск, который приходится на единицу доходности.
Коэффициент вариации отражает риск, который приходится на единицу доходности.


