Эффективные портфели ценных бумаг
Одно из важнейших понятий, связанных с анализом портфелей ценных бумаг, это выбор эффективных портфелей, определяемых как портфели, обеспечивающие наиболее высокую среднюю доходность при любой заданной степени риска, или наименьший риск при любой заданной доходности. Чтобы проиллюстрировать это понятие, предположим, что имеются два вида ценных бумаг, А и В, и что мы можем распределять средства между ними в любой пропорции. Предположим, что ожидаемая (средняя) доходность А составляет кА=5%, ее среднеквадратическое отклонение составляет Чтобы построить достижимое множество, нам потребуется коэффициент корреляции доходности этих активов rAB. Мы рассмотрим три различных его значения (rAB=+1,0, rAB=0 и rAB=-1,0) и для каждого случая рассчитаем среднюю доходность кР и среднеквадратическое отклонение Чтобы вычислить кР, мы используем формулу 6.5, а для нахождения значения
кР= В табл. 6.2 приведены результаты расчетов кР и При этом важно обратить внимание на следующие моменты. 1. Во всех трех случаях средняя ожидаемая доходность портфеля ценных бумаг возрастает линейно с 5 до 8% с ростом доли актива В в портфеле. Отметим также, что ожидаемая доходность портфеля не зависит от корреляции его активов.
2. Какие же из достижимых портфелей следует считать эффективными? Ответ прост: в случае rAB=+1,0, все портфели оказываются таковыми, а в случаях rAB=0 и rAB=-1,0 эффективной будет лишь часть достижимого множества от точки Y до B. Здесь Y обозначает портфель с наименьшей достижимой вариацией (наименьшим риском) . Участок дуги от А до Y соответствует неэффективным портфелям, поскольку для любого портфеля на АY найдется портфель на участке YВ с тем же риском, но большей средней доходностью. Следовательно, ни один рациональный инвестор не будет держать свои активы в портфелях ценных бумаг, изображенных на участке достижимого множества АY. 3. В одном крайнем случае (rAB=-1,0) риск может быть полностью устранен с помощью диверсификации: в этом случае
|

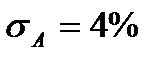 , доходность В кВ=8% и
, доходность В кВ=8% и  . Нашей задачей будет определить множество достижимых портфелей ценных бумаг, а затем из этого множества выделить подмножество эффективных портфелей.
. Нашей задачей будет определить множество достижимых портфелей ценных бумаг, а затем из этого множества выделить подмножество эффективных портфелей. доходности портфеля.
доходности портфеля. (6.5)
(6.5) = 1,00, 0,75, 0,50 и 0,00, а на рис. 6.2. представлены множества достижимых портфелей ценных бумаг для каждого случая.
= 1,00, 0,75, 0,50 и 0,00, а на рис. 6.2. представлены множества достижимых портфелей ценных бумаг для каждого случая.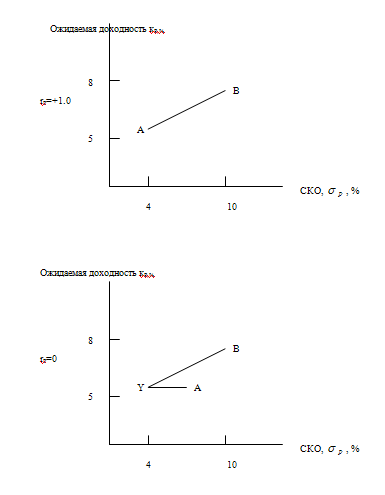

 = 0, в то время как в случае rAB=+1,0 диверсификация портфеля не позволяет полностью исключить риск. В промежуточных случаях диверсификация позволяет снизить, но не полностью устранить риск портфеля.
= 0, в то время как в случае rAB=+1,0 диверсификация портфеля не позволяет полностью исключить риск. В промежуточных случаях диверсификация позволяет снизить, но не полностью устранить риск портфеля.


