Теория градиентного переноса примесей (К-теория).
Теория градиентного переноса представляет собой обширный класс моделей, которые базируются на фикковской теории диффузии. Данная теория основана на применении дифференциальных уравнений, описывающих турбулентное движение в атмосфере и его влияние на рассеивание атмосферных примесей. По своей сути теория градиентного переноса является эйлеровой, поскольку рассматривает свойства движения жидкости относительно системы координат, фиксированной в пространстве. С точки зрения теории градиентного переноса диффузия в фиксированной точке пропорциональна градиенту концентрации. Математическая схема данной теории взята из физики тепло- и электропроводности. Уравнение (7.1) впервые было предложено Фикком. Записанное в одномерном случае, оно показывает, что степень изменения некоторого параметра q зависит от степени изменения его градиента и некоторой постоянной, которая в атмосфере называется коэффициентом турбулентной диффузии:
где: К - коэффициент турбулентной диффузии; q - среднее значение концентрации некоторого параметра воздуха в единице массы. В трехмерной пространственной форме для некоторой точки на поверхности земли уравнение турбулентной диффузии принимает вид:
Уравнение (7.2) выражает в дифференциальной форме закон сохранения вещества q. Ось х направлена по направлению ветра, ось z – вверх, t - время, с; U - скорость ветра, м/с; Кх, Ку, Кг - коэффициенты турбулентной диффузии по направлениям х, у, z, м/с. Многочисленные решения уравнения (7.1) для различных условий внесли вклад в развитие теории, которая получила название К-теория. Основой развития К-теории послужило существование большого числа решений уравнения Фикка с различными граничными условиями в классической теории теплопроводности. Основой многих решений является предположение равенства нулю потока примеси у поверхности земли. Дальнейшее развитие К-теории заключалось в учете влияния шероховатости подстилающей поверхности на основе введения: - степенной зависимости для профиля ветра, максимально приближенной к логарифмической; - характеристик атмосферной устойчивости, что позволило получить решение для бесконечного линейного источника, расположенного на поверхности земли, для бесконечного приподнятого линейного источника, расположенного под прямым углом к направлению ветра и для бесконечного приподнятого линейного источника, ориентированного вдоль среднего ветра со скоростью U. Уравнение турбулентной диффузии (7.2) является параболическим. Следовательно, в соответствии с ним, загрязнение при выходе из источника мгновенно распространяется по всему пространству и может быть обнаружено, хотя бы в совершенно малом количестве, на сколь угодно большом расстоянии от источника. В некоторых случаях (например, вблизи реальных границ облака загрязнения) использование параболического уравнения диффузии может привести к существенным ошибкам. Фундаментальное решение уравнения турбулентной диффузии, нашедшее широкое применение, выражено через функцию Гаусса и имеет вид:
где х - расстояние от центра диффузионного облака, м. Поскольку зависимость от x квадратичная, функция является симметричной. Коэффициенты а и b получены с помощью уравнения неразрывности, которое дает полную мощность выброса Q. Следовательно, для мгновенного точечного источника мощностью Q в момент времени t =0, решение уравнения (7.3) в одномерном случае имеет вид:
при условии U = const. Для получения гауссового уравнения распределения концентраций примеси у поверхности земли для уравнений К-теории следует ввести ряд ограничений: - решение не зависит от времени; - скорость ветра не меняется ни поперек общего потока, ни вертикально; - коэффициенты диффузии не зависят от местоположения (т.е. не являются функцией координат), хотя в реальной атмосфере это не так; - диффузия в направлении оси х мала по сравнению со средним потоком или Коэффициенты турбулентной диффузии в К-теории, используемые различными авторами, определены эмпирическим путем и зависят от высоты над поверхностью земли и числа Ричардсона (безразмерного градиента температуры). Число Ричардсона является функцией устойчивости или неустойчивости атмосферы и определяется следующим соотношением:
где: g - ускорение свободного падения, м/с2; Т - средняя температура воздуха в слое ¶ z ,°C; (¶Ө/¶z) - градиент температуры; ( ¶ и/ ¶ z) - вертикальный градиент скорости ветра. В моделях К-теории для вертикальной диффузии используются те же коэффициенты, что и для горизонтальной. Считается, что струя рассеивается в виде конуса и в целом симметрична. Наиболее упрощенная форма определения коэффициентов диффузии может быть представлена следующим образом:
где: σӨ - стандартное отклонение угловых колебаний флюгера, u, v, w - ортогональные компоненты скорости ветра соответственно по направлениям: запад-восток, север-юг, вертикаль. На основе уравнений (7.5) и (7.6) получены следующие формулы для определения коэффициентов диффузии:
Использование К-теории для инженерных задач основано на применении машинных программ, разработанных для задач рассеивания, причем расчет коэффициентов диффузии является частью этих программ. Правильность К-теории была доказана сопоставлением расчетов и результатов измерений процесса рассеивания в атмосфере. В настоящее время К-теория используется в основном для таких территорий, как города, где обычно наблюдаются слабые градиенты и имеется большое количество поверхностных (площадных и линейных) источников.
|

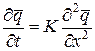 (7.1)
(7.1) (7.2)
(7.2) , (7.3)
, (7.3)
 (7.4)
(7.4)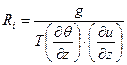 (7.5)
(7.5) (7.6)
(7.6)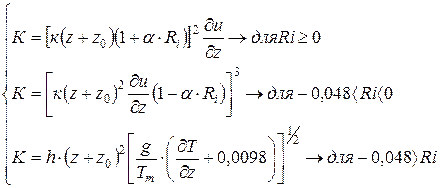 (7.7)
(7.7)


