Факторный анализ. Идея метода состоит в сжатии матрицы признаков в матрицу с меньшим числом переменных, сохраняющую почти ту же самую информацию
Идея метода состоит в сжатии матрицы признаков в матрицу с меньшим числом переменных, сохраняющую почти ту же самую информацию, что и исходная матрица. В основе моделей факторного анализа лежит гипотеза, что наблюдаемые переменные являются косвенными проявлениями небольшого числа скрытых (латентных) факторов. Под моделью факторного анализа понимают представление исходных переменных в виде линейной комбинации факторов. Х1 Х2..... Хn F1 ... Fm ┌──┬──┬──┬──┬──┐ ┌──┬──┬──┐; │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │; └──┴──┴──┴──┴──┘ └──┴──┴──┘; Рис. 7.1. Сжатие признакового пространства с применением факторного анализа Факторы F построены так, чтобы наилучшим способом (с минимальной погрешностью) представить Х. В этой модели «скрытые» переменные Fk называются общими факторами, а переменные Ui – специфическими факторами («специфический» – это лишь одно из значений используемого в англоязычной литературе слова unique, в отечественной литературе в качестве определения Ui встречаются также слова «характерный», «уникальный»). Значения aik называются факторными нагрузками. Обычно (хотя и не всегда) предполагается, что Xi стандартизованы (s i =1, Xi =0), а факторы F 1, F 2, …, Fm независимы и не связаны со специфическими факторами Ui (существуют модели, выполненные в других предположениях). Предполагается также, что факторы Fi стандартизованы. В этих условиях факторные нагрузки aik совпадают с коэффициентами корреляции между общими факторами и переменными Xi. Дисперсия Xi раскладывается на сумму квадратов факторных нагрузок и дисперсию специфического фактора:
Величина В соответствии с постановкой задачи необходимо искать такие факторы, при которых суммарная общность максимальна, а специфичность – минимальна.
|


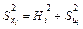 , где
, где  .
. называется общностью,
называется общностью,  – специфичностью. Другими словами, общность представляет собой часть дисперсии переменных, объясненную факторами, специфичность – часть не объясненной факторами дисперсии.
– специфичностью. Другими словами, общность представляет собой часть дисперсии переменных, объясненную факторами, специфичность – часть не объясненной факторами дисперсии.


