Решение уравнения с использованием логита
Решение такого уравнения упрощенно можно представить следующим образом 1. Получаются агрегированные данные по переменным x, в которых для каждой группы, характеризуемой значениями xj = 2. На агрегированных данных оцениваются коэффициенты уравнения Z = B 0 + B 1 x 1 + … + Bp x p. К сожалению, дисперсия Z здесь зависит от значений x, поэтому при использовании логита применяется специальная техника оценки коэффициентов – взвешенной регрессии. Еще одна особенность состоит в том, что в реальных данных очень часто группы по x оказываются однородными по y, поэтому оценки В некоторых статистических пакетах такие группы объектов просто-напросто отбрасываются. В настоящее время в статистическом пакете для оценки коэффициентов используется метод максимального правдоподобия, лишенный этого недостатка. Тем не менее проблема, хотя и не в таком остром виде, остается: если оценки вероятности для многих групп оказываются равными 0 или 1, оценки коэффициентов регрессии имеют слишком большую дисперсию. Поэтому, имея в качестве независимых переменных такие признаки, как душевой доход в сочетании с возрастом, их следует укрупнить по интервалам, приписав объектам средние значения интервалов.
|
, подсчитывается доля объектов, соответствующих событию { y =1}. Эта доля является оценкой вероятности 
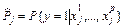. В соответствии с этим для каждой группы получается значение логита Zj.
оказываются равными 0 или 1. Таким образом, оценка логита для них не определена (для этих значений 
).
