Классическая линейная модель регрессионного анализа

В линейной модели предполагается, что зависимая переменная y связана со значениями независимых показателей x^k (факторов) формулой [2]

.

Традиционные названия «зависимая» для y и «независимые» для x^k отражают не столько статистический смысл, сколько их содержательную интерпретацию.

Величина e _i называется ошибкой регрессии. В классической модели предполагается, что регрессионные ошибки независимы и распределены нормально с параметрами N (0,σ²). Кроме того, в данной модели мы рассматриваем переменные x как неслучайные значения. Такое на практике получается, когда идет активный эксперимент, в котором задают значения x (например, назначили зарплату работнику), а затем измеряют y (оценили, какой стала производительность труда). Поэтому зависимую переменную иногда называют откликом. Теория регрессионных уравнений со случайными независимыми переменными сложнее, но известно, что при большом числе наблюдений использование метода, разработанного для случайных X, корректно.

Для получения выборочных оценок b_k коэффициентов B_k регрессии минимизируется сумма квадратов ошибок регрессии:

.

Решение задачи сводится к решению системы линейных уравнений относительно b_k.

На основании оценок регрессионных коэффициентов рассчитываются оценки значений y:

.

По сути дела, эти оценки являются оценками математического ожидания Y при заданных значениях X.

О качестве полученного уравнения регрессии можно судить, исследовав – оценки случайных ошибок уравнения. Оценка дисперсии случайной ошибки получается по формуле .

Величина S называется стандартной ошибкой регрессии. Чем меньше величина S, тем лучше уравнение регрессии описывает независимую переменную y.

Так как мы ищем оценки b _k, используя случайные данные, то они, в свою очередь, будут представлять случайные величины. В связи с этим возникают вопросы:

1. Существует ли регрессионная зависимость? Может быть, все коэффициенты регрессии в генеральной совокупности равны нулю, оцененные их значения ненулевые только благодаря случайным отклонениям данных?

2. Существенно ли влияние на зависимую переменную отдельных независимых переменных?

В пакете вычисляются статистики, позволяющие решить эти задачи.

6.1.1. Существует ли линейная регрессионная зависимость?

Для проверки одновременного отличия всех коэффициентов регрессии от нуля проведем анализ квадратичного разброса значений зависимой переменной относительно среднего. Его можно разложить на две суммы следующим образом:

.

В этом разложении обычно обозначают:

– общую сумму квадратов отклонений;

– сумму квадратов регрессионных отклонений;

– разброс по линии регрессии.

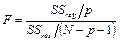Статистика в условиях гипотезы равенства нулю регрессионных коэффициентов имеет распределение Фишера, и, естественно, по этой статистике проверяют, являются ли коэффициенты B ₁, …, B _p одновременно нулевыми. Если наблюдаемая значимость статистики Фишера мала (например, sig F =0,003), то это означает, что данные распределены вдоль линии регрессии и гипотеза отвергается; если значимость велика (например, Sign F =0,12), то, следовательно, данные не связаны такой линейной связью, гипотеза не отвергается.