Ответ: 5.
Ответ: 5
8. B 5 № 27947.  Найдите радиус окружности, описанной около прямоугольника
Найдите радиус окружности, описанной около прямоугольника  , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.
Решение.
Радиус окружности, описанной около прямоугольника, равен половине его диагонали. Диагональ равна 5, поэтому радиус равен 2,5.
Ответ: 2,5.
Ответ: 2,5
9. B 5 № 27733.  Найдите квадрат длины вектора
Найдите квадрат длины вектора  .
.
Решение.
Имеем:  ,
,  . Координаты разности векторов равны разности соответствующих координат, поэтому
. Координаты разности векторов равны разности соответствующих координат, поэтому  . Длина вектора
. Длина вектора 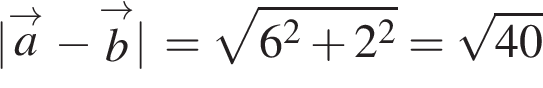 . Поэтому квадрат длины вектора равен
. Поэтому квадрат длины вектора равен  .
.
Ответ: 40.
Ответ: 40
10. B 5 № 245008.  Найдите (в см2) площадь
Найдите (в см2) площадь  фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
.
Вариант № 3658380
1. B 5 № 27824.  Две стороны параллелограмма относятся как
Две стороны параллелограмма относятся как  , а периметр его равен 70. Найдите большую сторону параллелограмма.
, а периметр его равен 70. Найдите большую сторону параллелограмма.
Решение.
Противоположные стороны параллелограмма попарно равны, значит,
 .
.
Зная, что периметр параллелограмма равен 70, находим:  .
.
Ответ: 20.
Ответ: 20
B 5 № 27546.
 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
 Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Поэтому
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Поэтому
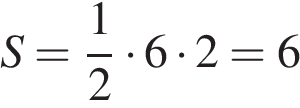 см2.
см2.
Ответ: 6.
Ответ: 6
3. B 5 № 27821.  Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Решение.
больший отрезок средней линии трапеции является средней линией треугольника  , а значит, равен половине его основания.
, а значит, равен половине его основания.
 .
.
Ответ: 5.
Ответ: 5
4. B 5 № 27815.  В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата.
В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата.
Решение.
 В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а его периметр 56.
В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а его периметр 56.
Ответ: 56.
Ответ: 56
B 5 № 27600.
 Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Решение.
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a+3. Периметр будет соответственно равен
P = 2  a + 2
a + 2  (a + 3) = 18,
(a + 3) = 18,
тогда одна из сторон будет равна 3, а другая 6. Поэтому
S = 3  6 = 18.
6 = 18.
Ответ: 18.
Ответ: 18
6. B 5 № 27549.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
 Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
 см2.
см2.
Ответ: 12.
Ответ: 12
7. B 5 № 27814. 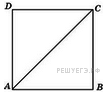 Найдите сторону квадрата, диагональ которого равна
Найдите сторону квадрата, диагональ которого равна  .
.
Решение.
По теореме Пифагора 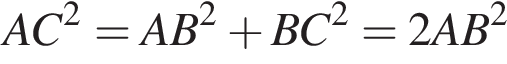 , значит,
, значит,
 .
.
Ответ: 2.
Ответ: 2
B 5 № 27586.
 Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°
Решение.
Площадь ромба равна произведению квадрата его стороны и синуса его угла. Поэтому
 см2.
см2.
Ответ: 0,5.
Ответ: 0,5
B 5 № 27656.
 Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Решение.
Координаты точки, делящей отрезок пополам, считаются по формуле:
 ,
, 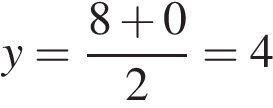
Ответ: 4.
Ответ: 4
10. B 5 № 244991.  Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
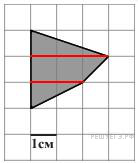 Площадь четырехугольника равна сумме площадей двух прямоугольных треугольников и площади трапеции. Поэтому
Площадь четырехугольника равна сумме площадей двух прямоугольных треугольников и площади трапеции. Поэтому

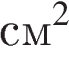 .
.
Ответ: 5
Решение.
 Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда
Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда
 .
.
Поэтому
 .
.
Ответ: 3
Решение.
так как 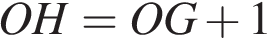 , то
, то  . Тогда
. Тогда
 ,
,
откуда,  .
.
Ответ: 6.
Ответ: 6
Вариант № 3658424
1. B 5 № 27555.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Решение.
 Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому
Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому
 см2.
см2.
Ответ: 6.
Ответ: 6
2. B 5 № 244989.  Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.

Площадь четырехугольника равна разности площади большого прямоугольного треугольника и маленького прямоугольного треугольника, гипотенуза которого является стороной исходного четырехугольника. Поэтому

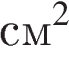 .
.
Ответ: 2,5
B 5 № 27748.
 В треугольнике
В треугольнике 
 . Внешний угол при вершине
. Внешний угол при вершине 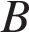 равен
равен  . Найдите угол
. Найдите угол 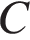 . Ответ дайте в градусах.
. Ответ дайте в градусах.
Решение.
так как треугольник  равнобедренный, то углы при его основании равны.
равнобедренный, то углы при его основании равны.
 .
.
Ответ: 69.
Ответ: 69
4. B 5 № 27714.  Диагонали изображенного на рисунке ромба
Диагонали изображенного на рисунке ромба  равны 12 и 16. Найдите длину вектора
равны 12 и 16. Найдите длину вектора  +
+  .
.
Решение.
Длина вектора  равна вектору
равна вектору  . Длина вектора
. Длина вектора  равна
равна  .
.
Ответ: 16.
Ответ: 16
5. B 5 № 27547.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Выберем за основание вертикальную сторону, длиной 3 клетки. Тогда проведенная к ней из левой нижней вершины труегольника высота равна 5 клеткам (см. рис.). Поэтому
 см2.
см2.
Ответ: 7,5.
Ответ: 7,5
6. B 5 № 319057. Площадь параллелограмма  равна 176. Точка
равна 176. Точка  – середина стороны
– середина стороны  . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
Решение.
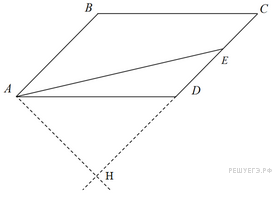
Пусть  − перпендикуляр, опущенный из точки
− перпендикуляр, опущенный из точки  на продолжение стороны
на продолжение стороны  Выразим площадь треугольника
Выразим площадь треугольника  через площадь параллелограмма
через площадь параллелограмма 

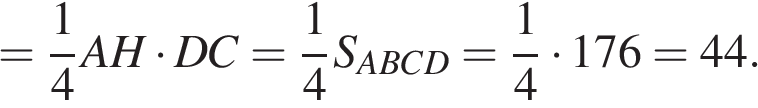
Ответ: 44.
Ответ: 44
7. B 5 № 27690.  Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
Решение.
Решая совместно эти два уравнения, получаем, что x = 6, y = −6.
Ответ: −6.
Ответ: -6
8. B 5 № 27717.  Диагонали ромба
Диагонали ромба  пересекаются в точке
пересекаются в точке  и равны 12 и 16. Найдите длину вектора
и равны 12 и 16. Найдите длину вектора  +
+ 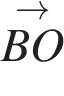 .
.
Решение.
Сумма векторов  +
+ 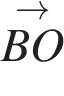 равна вектору
равна вектору  .
.  — ромб, его диагонали пересекаются под прямым углом, значит,
— ромб, его диагонали пересекаются под прямым углом, значит,
 .
.
Ответ: 10.
Ответ: 10
9. B 5 № 27564.  Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
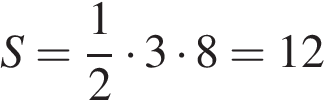 см2.
см2.
Ответ: 12.
Ответ: 12
10. B 5 № 27453.  Найдите тангенс угла
Найдите тангенс угла  .
.
Вариант № 3658517
1. B 5 № 27450.  Найдите тангенс угла
Найдите тангенс угла  .
.
Решение.
 проведем высоту
проведем высоту  из точки
из точки 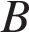 на сторону
на сторону  . Тогда, принимая во внимание, что
. Тогда, принимая во внимание, что  , получим:
, получим:
 .
.
Ответ: 1.
Ответ: 1
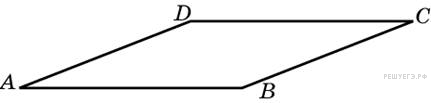
2. B 5 № 27552.  Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Решение.
 Площадь прямоугольника равна разности площади прямоугольника и четырех прямоугольных треугольников, гипотенузы которых являются сторонами исходного прямоугольника. Поэтому
Площадь прямоугольника равна разности площади прямоугольника и четырех прямоугольных треугольников, гипотенузы которых являются сторонами исходного прямоугольника. Поэтому
 см2.
см2.
Ответ: 10.
Примечание
Для вычисления площади фигуры можно сложить площади треугольников BCD и BAD, имеющих общую сторону BD, длина которой равна 5, и равные проведенные к ней высоты длины 2.
Ответ: 10
B 5 № 27669.
 Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Решение.
Уравнение прямой имеет вид 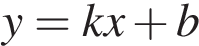 , где
, где 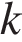 — угловой коэффициент, равный тангенсу угла наклона прямой к оси абсцисс. Угловой коэффициент прямой a отрицателен и равен
— угловой коэффициент, равный тангенсу угла наклона прямой к оси абсцисс. Угловой коэффициент прямой a отрицателен и равен  . Прямые а и b параллельны, поэтому их угловые коэффициенты равны. Следовательно, уравнение прямой b имеет вид
. Прямые а и b параллельны, поэтому их угловые коэффициенты равны. Следовательно, уравнение прямой b имеет вид  .
.
Точка  лежит на прямой b, поэтому
лежит на прямой b, поэтому  , откуда
, откуда  . Тогда прямая b задается уравнением
. Тогда прямая b задается уравнением  . Осталось найти абсциссу точки пересечения b с осью абсцисс:
. Осталось найти абсциссу точки пересечения b с осью абсцисс:
 .
.
Приведем другое решение.
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Прямая b на оси ординат отсекает отрезок вдвое больше, чем прямая a. Следовательно, на оси абсцисс она тоже отсекает отрезок вдвое большей длины. Поэтому искомая абсцисса равна 12.
Ответ: 12.
Ответ: 12
4. B 5 № 27544.  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
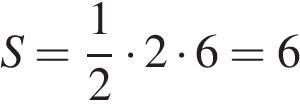 см2.
см2.
Ответ: 6.
Ответ: 6
5. B 5 № 27937. 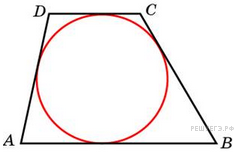 Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Решение.
 В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда 

Ответ: 10.
Ответ: 10
6. B 5 № 27938.  Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Решение.
В четырехугольник можно вписать окружность тогда и только тогда, когда 
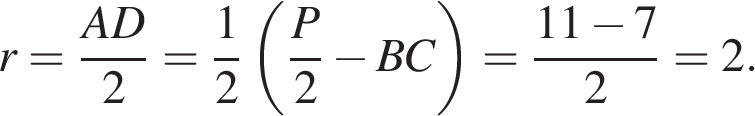
Ответ: 2.
Ответ: 2
7. B 5 № 27723.  Найдите сумму координат вектора
Найдите сумму координат вектора  .
.
Решение.
Координаты вектора равны разности координат конца вектора и его начала. Вектор  имеет координаты
имеет координаты  . Поэтому сумма координат вектора
. Поэтому сумма координат вектора  равна 8.
равна 8.
Ответ: 8.
Ответ: 8
8. B 5 № 27936.  Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Решение.
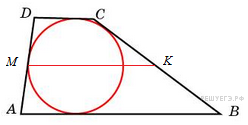
в выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда 

Ответ: 4.
Ответ: 4
B 5 № 245003.
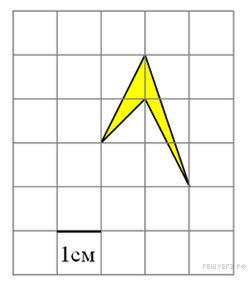 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Решение.
 Площадь четырехугольника равна разности площади большого прямоугольника, четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырехугольника и площади маленького квадрата. Поэтому
Площадь четырехугольника равна разности площади большого прямоугольника, четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырехугольника и площади маленького квадрата. Поэтому

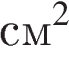 .
.
Примечание.
Заданный четырёхугольник можно рассматривать как два треугольника с общим основанием, равным длине квадратной клетки. Высоты этих треугольников равны 1, поэтому их площади 0,5, а сумма этих площадей равна 1.
Ответ: 1
10. B 5 № 27697.  Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Вариант № 3658576
1. B 5 № 27858. 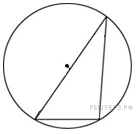 Найдите хорду, на которую опирается угол
Найдите хорду, на которую опирается угол  , вписанный в окружность радиуса 3.
, вписанный в окружность радиуса 3.
Решение.

 , значит,
, значит,  , т. к. является центральным углом, опирающимся на ту же хорду. Соответственно, треугольник
, т. к. является центральным углом, опирающимся на ту же хорду. Соответственно, треугольник  – равносторонний, так как
– равносторонний, так как  .
.

 Найдите радиус окружности, описанной около прямоугольника
Найдите радиус окружности, описанной около прямоугольника  , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1. Найдите квадрат длины вектора
Найдите квадрат длины вектора  .
. ,
,  . Координаты разности векторов равны разности соответствующих координат, поэтому
. Координаты разности векторов равны разности соответствующих координат, поэтому  . Длина вектора
. Длина вектора 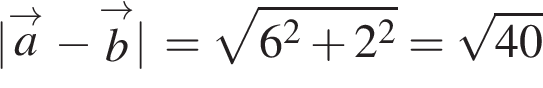 . Поэтому квадрат длины вектора равен
. Поэтому квадрат длины вектора равен  .
. Найдите (в см2) площадь
Найдите (в см2) площадь  фигуры, изображенной на клетчатой бумаге с размером клетки 1 см
фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
. Две стороны параллелограмма относятся как
Две стороны параллелограмма относятся как  , а периметр его равен 70. Найдите большую сторону параллелограмма.
, а периметр его равен 70. Найдите большую сторону параллелограмма. .
. .
. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Поэтому
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию или его продолжению. Поэтому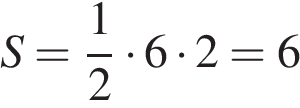 см2.
см2. Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей. , а значит, равен половине его основания.
, а значит, равен половине его основания. .
. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата.
В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 7. Найдите периметр этого квадрата. В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а его периметр 56.
В квадрате расстояние от точки пересечения диагоналей до стороны равно половине стороны. Поэтому сторона квадрата равна 14, а его периметр 56. Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой. a + 2
a + 2  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади большого квадрата, маленького квадрата и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому см2.
см2. Найдите сторону квадрата, диагональ которого равна
Найдите сторону квадрата, диагональ которого равна  .
.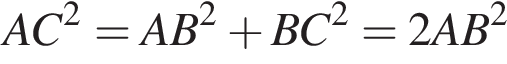 , значит,
, значит, .
. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150° см2.
см2. Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8). ,
, 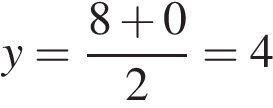
 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  Площадь четырехугольника равна сумме площадей двух прямоугольных треугольников и площади трапеции. Поэтому
Площадь четырехугольника равна сумме площадей двух прямоугольных треугольников и площади трапеции. Поэтому
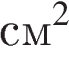 .
. Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда
Площадь кольца равна разности площади большого и малого кругов. Радиус большого круга равен 2, а малого — 1, откуда .
. .
.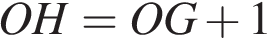 , то
, то  . Тогда
. Тогда ,
, .
. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому
Площадь фигуры равна разности площади прямоугольника и трех треугольников. Поэтому см2.
см2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 

 В треугольнике
В треугольнике 
 . Внешний угол при вершине
. Внешний угол при вершине 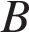 равен
равен  . Найдите угол
. Найдите угол 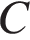 . Ответ дайте в градусах.
. Ответ дайте в градусах. .
. Диагонали изображенного на рисунке ромба
Диагонали изображенного на рисунке ромба  +
+  .
. равна вектору
равна вектору  . Длина вектора
. Длина вектора  .
. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  см2.
см2. – середина стороны
– середина стороны  . Найдите площадь треугольника
. Найдите площадь треугольника  .
.
 − перпендикуляр, опущенный из точки
− перпендикуляр, опущенный из точки  на продолжение стороны
на продолжение стороны  Выразим площадь треугольника
Выразим площадь треугольника 

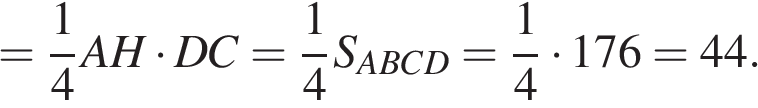
 Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x.
Найдите ординату точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = − x. Диагонали ромба
Диагонали ромба  и равны 12 и 16. Найдите длину вектора
и равны 12 и 16. Найдите длину вектора  +
+ 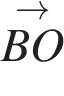 .
. .
. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).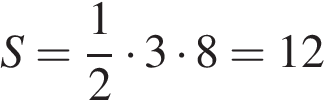 см2.
см2. Найдите тангенс угла
Найдите тангенс угла  .
. Найдите тангенс угла
Найдите тангенс угла  проведем высоту
проведем высоту  из точки
из точки  . Тогда, принимая во внимание, что
. Тогда, принимая во внимание, что  , получим:
, получим: .
. Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1.
Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. Площадь прямоугольника равна разности площади прямоугольника и четырех прямоугольных треугольников, гипотенузы которых являются сторонами исходного прямоугольника. Поэтому
Площадь прямоугольника равна разности площади прямоугольника и четырех прямоугольных треугольников, гипотенузы которых являются сторонами исходного прямоугольника. Поэтому см2.
см2. Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox
Прямая a проходит через точки с координатами (0; 4) и (6; 0). Прямая b проходит через точку с координатами (0; 8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox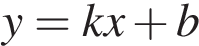 , где
, где 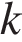 — угловой коэффициент, равный тангенсу угла наклона прямой к оси абсцисс. Угловой коэффициент прямой a отрицателен и равен
— угловой коэффициент, равный тангенсу угла наклона прямой к оси абсцисс. Угловой коэффициент прямой a отрицателен и равен  . Прямые а и b параллельны, поэтому их угловые коэффициенты равны. Следовательно, уравнение прямой b имеет вид
. Прямые а и b параллельны, поэтому их угловые коэффициенты равны. Следовательно, уравнение прямой b имеет вид  .
. лежит на прямой b, поэтому
лежит на прямой b, поэтому  , откуда
, откуда  . Тогда прямая b задается уравнением
. Тогда прямая b задается уравнением  . Осталось найти абсциссу точки пересечения b с осью абсцисс:
. Осталось найти абсциссу точки пересечения b с осью абсцисс: .
. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см 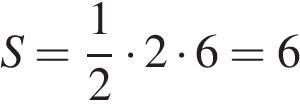 см2.
см2. Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию.
Около окружности описана трапеция, периметр которой равен 40. Найдите ее среднюю линию. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда 

 Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.
Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.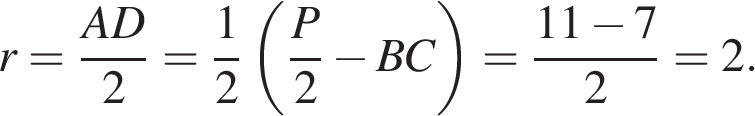
 Найдите сумму координат вектора
Найдите сумму координат вектора  . Поэтому сумма координат вектора
. Поэтому сумма координат вектора  Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.
Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  Площадь четырехугольника равна разности площади большого прямоугольника, четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырехугольника и площади маленького квадрата. Поэтому
Площадь четырехугольника равна разности площади большого прямоугольника, четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырехугольника и площади маленького квадрата. Поэтому
 Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4).
Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (−2; −2), (6; −2), (6; 4), (−2; 4). Найдите хорду, на которую опирается угол
Найдите хорду, на которую опирается угол  , вписанный в окружность радиуса 3.
, вписанный в окружность радиуса 3.
 , значит,
, значит,  , т. к. является центральным углом, опирающимся на ту же хорду. Соответственно, треугольник
, т. к. является центральным углом, опирающимся на ту же хорду. Соответственно, треугольник  .
.


