Решение. 37 страница
Решение. Рассмотрим два варианта.
Стоимость каменного фундамента складывается из стоимости камня 9
Стоимость бетонного фундамента складывается из стоимости цемента 50
Стоимость самого дешевого варианта составляет 15 900 рублей.
Ответ: 15 900. Ответ: 15900 5. B 4. В среднем гражданин А. в дневное время расходует 120 кВт Решение. Рассмотрим оба типа счётчиков.
При использовании однотарифного счётчика, гражданин А. платил в месяц
(120 кВт
При использовании двухтарифного счётчика, гражданин А. платит в месяц
120 кВт
Установка нового типа счётчика позволяет экономить 732 − 399 = 333 руб. в месяц или 333 Ответ: 3996 6. B 4. Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость такой покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.
Решение. Рассмотрим все варианты.
При покупке у поставщика A стоимость заказа складывается из стоимости бруса 4200
При покупке у поставщика Б стоимость бруса составляет 4800
При покупке у поставщика В стоимость заказа складывается из стоимости бруса 4300
Стоимость самого дешевого варианта составляет 178 200 рублей.
Ответ: 178 200. Ответ: 178200 7. B 4. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены
В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.
Решение. Рассмотрим все варианты.
Модель А: Модель Б: Модель В: Модель Г:
Таким образом, наивысший рейтинг имеет модель А. Он равен 1.
Ответ: 1. Ответ: 1 8. B 4. Автомобильный журнал определяет рейтинги автомобилей на основе показателей безопасности
В таблице даны оценки каждого показателя для трёх моделей автомобилей. Определите наивысший рейтинг представленных в таблице моделей автомобилей.
Решение. Рассмотрим все варианты.
Модель А: Модель Б: Модель В:
Тем самым, наивысший рейтинг имеет имеет модель В, он равен 0,82
Ответ: 0,82. Ответ: 0,82 9. B 4. Для строительства гаража можно использовать один из двух типов фундамента: бетонный или фундамент из пеноблоков. Для фундамента из пеноблоков необходимо 4 кубометра пеноблоков и 2 мешка цемента. Для бетонного фундамента необходимо 4 тонны щебня и 40 мешков цемента. Кубометр пеноблоков стоит 2550 рублей, щебень стоит 580 рублей за тонну, а мешок цемента стоит 210 рублей. Сколько рублей будет стоить материал, если выбрать наиболее дешевый вариант? Решение. Рассмотрим все варианты.
Стоимость фундамента из пеноблоков складывается из стоимости пеноблоков 4
Стоимость бетонного фундамента складывается из стоимости цемента 40
Первый вариант дешевле второго.
Ответ: 10 620. Ответ: 10620 10. B 4. При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 9 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1 600 рублей, щебень стоит 780 рублей за тонну, а мешок цемента стоит 230 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?
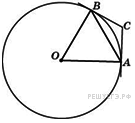
Вариант № 3657611 1. B 5 № 27880. Решение. угол между касательной и хордой равен половине дуги, стягиваемой хордой, рассмотрим треугольник
Ответ: 58. Ответ: 58 2.B 5 № 27585. Решение. Площадь параллелограмма равна произведению его сторон на синус угла между ними. Поэтому
Ответ: 40. Ответ: 40 3. B 5 № 27563. Решение. Площадь прямоугольного треугольника равна половине произведения катетов
Ответ: 12. Ответ: 12 4.B 5 № 27600. Решение. Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a+3. Периметр будет соответственно равен P = 2 тогда одна из сторон будет равна 3, а другая 6. Поэтому S = 3 Ответ: 18. Ответ: 18 5.B 5 № 27580. Решение.
Ответ: 8. Ответ: 8 6. B 5 № 27908. Решение.
значит, Ответ: 18.
Приведем другое решение. Высота правильного треугольника равна 3 радиусам вписанной окружности, поэтому она равна 18. Ответ: 18 7. B 5 № 27692. Решение.
Ответ: 10. Ответ: 10 8. B 5 № 27575. Решение.
Ответ: 14. Ответ: 14 9. B 5 № 27745. Решение. так как треугольник
Ответ: 31. Ответ: 31 10. B 5 № 27846. Решение.
Ответ: 4. Ответ: 4
Вариант № 3657662 1.B 5 № 27595. Решение. Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Пусть периметр и площадь меньшего многоугольника соответственно равны P 1 и S 1, периметр и площадь большего многоугольника соответственно равны P 2 и S 2. Поэтому
откуда
Поэтому S 2 = 50.
Ответ: 50. Ответ: 50 2.B 5 № 27707. Решение. Вектор
Ответ: 10. Ответ: 10 3.B 5 № 27772. Решение. так как
Ответ: 42.
Ответ: 42 4. B 5 № 27712. Решение. Разность векторов
Ответ: 8. Ответ: 8 5.B 5 № 27675. Решение.
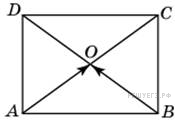
Противоположные стороны попарно равны, четырехугольник является параллелограммом, значит, точка P является серединой отрезка CB. Поэтому координаты точки P вычисляются следующим образом:
Ответ: 4. Ответ: 4 6.B 5 № 27845. Решение. Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,
Ответ: 9. Ответ: 9 7.B 5 № 27656. Решение. Координаты точки, делящей отрезок пополам, считаются по формуле:
Ответ: 4. Ответ: 4 8. B 5 № 27708. Решение. Сумма векторов
Ответ: 10. Ответ: 10 9.B 5 № 27594. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Средняя линия трапеции равна полусумме оснований. Поэтому
Ответ: 6. Ответ: 6 10.B 5 № 27832.
Вариант № 3657799 1.B 5 № 27671. Решение. Уравнение прямой имеет вид:
Так как прямые параллельны, то
Теперь подставляя значения
|

 1450 = 13 050 руб., а также стоимости цемента 13
1450 = 13 050 руб., а также стоимости цемента 13  и оценок функциональности
и оценок функциональности 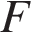 , качества
, качества 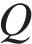 и дизайна
и дизайна 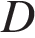 . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
. Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле
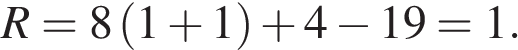
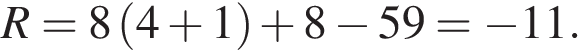
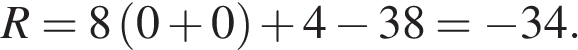

 , комфорта
, комфорта 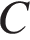 , функциональности
, функциональности 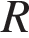 вычисляется по формуле
вычисляется по формуле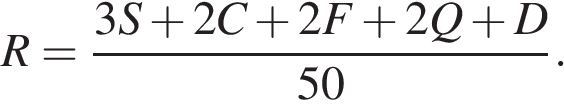

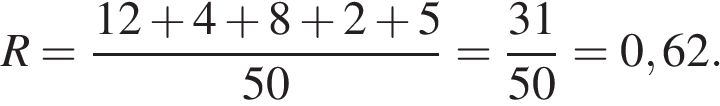
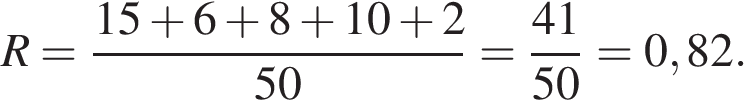
 Касательные
Касательные  и
и  к окружности образуют угол
к окружности образуют угол  , равный
, равный  . Найдите величину меньшей дуги
. Найдите величину меньшей дуги  , стягиваемой точками касания. Ответ дайте в градусах.
, стягиваемой точками касания. Ответ дайте в градусах.

 Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.
Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.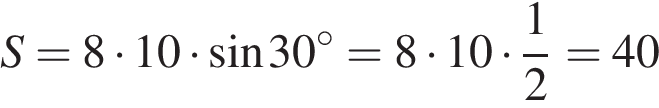 см2.
см2. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9).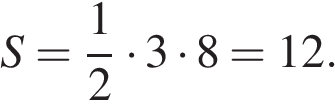
 Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой. a + 2
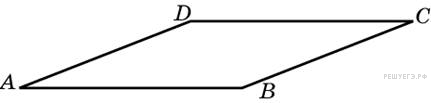
a + 2  Найдите площадь четырехугольника, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6).
Найдите площадь четырехугольника, вершины которого имеют координаты (6;3), (9;4), (10;7), (7;6).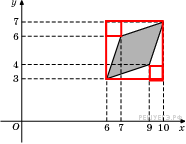 Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных треугольников с катетами 1 и 3 и двух равных квадратов 1х1. Поэтому
Площадь четырехугольника равна разности площади квадрата 4х4, четырех равных прямоугольных треугольников с катетами 1 и 3 и двух равных квадратов 1х1. Поэтому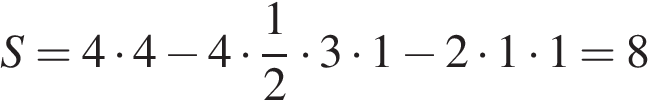 см2.
см2.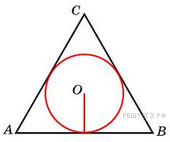 Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.

 Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус.
Окружность с центром в начале координат проходит через точку P (8; 6). Найдите ее радиус.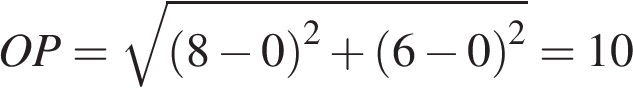 , а это и есть радиус окружности.
, а это и есть радиус окружности. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9).
Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9).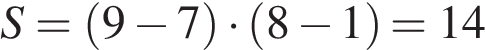 .
. В треугольнике
В треугольнике  угол
угол 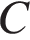 равен
равен 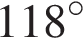 ,
,  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.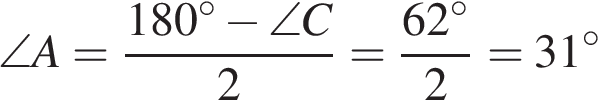 .
.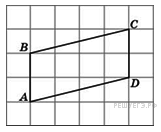 Найдите высоту параллелограмма
Найдите высоту параллелограмма  , опущенную на сторону
, опущенную на сторону  проведем высоту
проведем высоту  из вершины
из вершины  . По рисунку находим ее высоту.
. По рисунку находим ее высоту. Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника. ,
, ,
,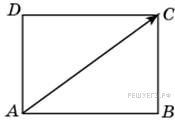 Две стороны прямоугольника
Две стороны прямоугольника  .
.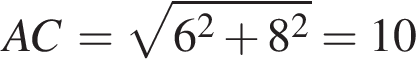 .
.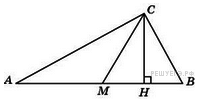 Острые углы прямоугольного треугольника равны
Острые углы прямоугольного треугольника равны  и
и 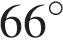 . Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах. – медиана, то
– медиана, то  (свойство медианы в прямоугольном треугольнике), а значит, углы
(свойство медианы в прямоугольном треугольнике), а значит, углы  равны как углы при основании равнобедренного треугольника.
равны как углы при основании равнобедренного треугольника.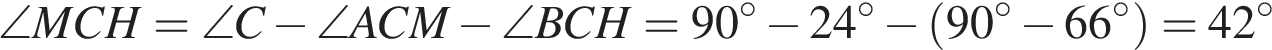 .
. Две стороны прямоугольника
Две стороны прямоугольника  .Найдите длину разности векторов
.Найдите длину разности векторов  и
и 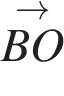 .
. . Длина вектора
. Длина вектора 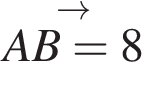 .
.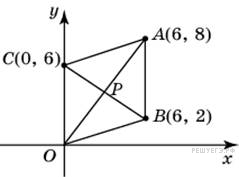 Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.
Точки O (0; 0), A (6; 8), B (6; 2), C (0; 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. ,
,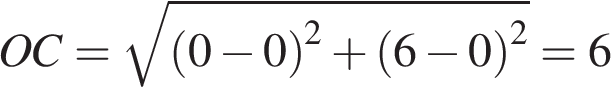 ,
,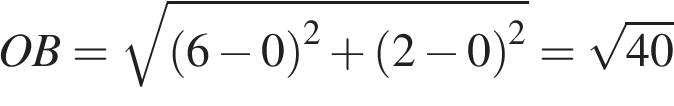 ,
, .
. ,
,  .
.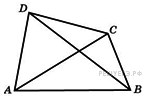 Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.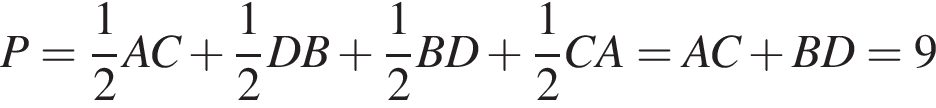 .
. Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
Найдите ординату середины отрезка, соединяющего точки O (0; 0) и A (6; 8).
 Две стороны прямоугольника
Две стороны прямоугольника  .
.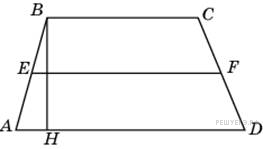 Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. см2.
см2.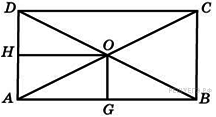 В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.
В прямоугольнике расстояние от точки пересечения диагоналей до меньшей стороны на 1 больше, чем расстояние от нее до большей стороны. Периметр прямоугольника равен 28. Найдите меньшую сторону прямоугольника.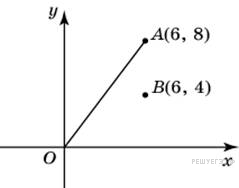 Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B (6; 4) и параллельной прямой, проходящей через начало координат и точку A (6; 8).
Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B (6; 4) и параллельной прямой, проходящей через начало координат и точку A (6; 8).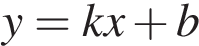 , где
, где 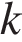 — угловой коэффициент. Тогда, подставляя значения абсцисс и ординат точек
— угловой коэффициент. Тогда, подставляя значения абсцисс и ординат точек 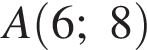 и
и  , решая уравнения одновременно, получаем:
, решая уравнения одновременно, получаем: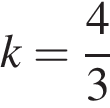 .
.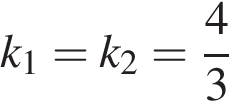 .
.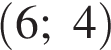 , зная еще, что координата второй точки, принадлежащей прямой,
, зная еще, что координата второй точки, принадлежащей прямой, 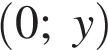 , находим
, находим 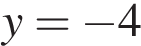 .
.


