Решение. 39 страница
Решение. В четырехугольник можно вписать окружность тогда и только тогда, когда
Ответ: 14. Ответ: 14 6. B 5 № 27689. Решение. Решая систему этих двух уравнений, получаем, что y = x = 1,2.
Ответ: 1,2. Ответ: 1,2 7. B 5 № 27456. Решение.
Примечание. Можно заметить и доказать, что равнобедренный треугольник ABO является прямоугольным. Тогда углы AOB и OАB равны 45°, а их тангенсы равны 1.
Ответ: 1. Ответ: 1 B 5 № 27836.
Решение. средняя линия трапеции равна:
Ответ: 10.
Ответ: 10 9. B 5 № 315122. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.
Решение. Площади кругов относятся как квадраты их радиусов. Поскольку радиус большего круга вдвое больше радиуса меньшего круга, площадь большего круга вчетверо больше площади меньшего. Следовательно, она равна 204. Площадь заштрихованной фигуры равна разности площадей кругов: 204 − 51 = 153.
Ответ: 153. Ответ: 153 10. B 5 № 27544. Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Ответ: 6. Ответ: 6 Вариант № 3658019 1. B 5 № 27682. Решение. Пусть точка P является серединой отрезков OA и BC. Координаты точки P вычисляются следующим образом:
но с другой стороны,
Поэтому
Ответ: 8. Ответ: 8 2. B 5 № 27665. Решение. Если опустить из точки
Тогда получается, что
Ответ: 0,8. Ответ: 0,8 3. B 5 № 27716. Решение. Разность векторов
Ответ: 10. Ответ: 10 4. B 5 № 315133. Решение.
Ответ:96. Ответ: 96 5. B 5 № 27544. Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Ответ: 6. Ответ: 6 6. B 5 № 245005. Решение.
Примечание. Данный четырёхугольник можно разбить на прямоугольный треугольник, с катетами 1 и 3, прямоугольную трапеию с основаниями 3 и 1 и прямоугольный треугольник с катетами 1 и 1. Поэтому его площадь равна 4. Ответ: 4 7. B 5 № 27737. Решение. Координаты вектора равны разности координат конца вектора и его начала. Поэтому вектор
Ответ: 200. Ответ: 200 8. B 5 № 27848. Решение.
Ответ: 3. Ответ: 3 9. B 5 № 27594. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Средняя линия трапеции равна полусумме оснований. Поэтому
Ответ: 6. Ответ: 6 10. B 5 № 27803. Решение.
Ответ: 3. Ответ: 3 Вариант № 3658107 1. B 5 № 77152. Решение. треугольники
Ответ: 5. Ответ: 5 B 5 № 245002.
Решение.
Ответ: 3 3. B 5 № 27545. Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Ответ: 12. Ответ: 12 4. B 5 № 27658. Решение. Координаты точки, делящей отрезок пополам, считаются по формуле:
Ответ: 5. Ответ: 5 5. B 5 № 27779. Решение. Угол между высотами равен углу между сторонами, к которым они проведены: Ответ: 82. Ответ: 82 6. B 5 № 27763. Решение. Cумма углов в выпуклом четырёхугольнике равна 360 градусам, следовательно,
Ответ: 130. Ответ: 130 7. B 5 № 27674. Решение. Так как у параллелограмма противоположные стороны попарно равны, то
Поэтому
Ответ: 6. Ответ: 6 8. B 5 № 27699. Решение. Треугольник является прямоугольным. Центр окружности, описанной около прямоугольного треугольника, совпадает с серединой гипотенузы. Тогда координаты центра окружности:
Ответ: 4. Ответ: 4 B 5 № 27794.
Решение. Высота в равнобедренном треугольнике является медианой, поэтому AH = 2. Рассмотрим треугольник AHC, по теореме Пифагора:
Угол АСН, лежащий против катета, равного половине гипотенузы, равен 30 Ответ: 60. Ответ: 60 10. B 5 № 27642. Решение. Площадь круга определяется формулой S = π R 2. Площадь кольца равна разности площадей первого и второго круга. Тогда
Поэтому площадь кольца: S = S 1 − S 2 = 16 − 4 = 12.
Ответ: 12. Ответ: 12 Вариант № 3658206 1. B 5 № 27740. Решение. Координаты вектора равны разности координат конца вектора и его начала. Поэтому вектор
Ответ: 40. Ответ: 40 B 5 № 27586.
Решение. Площадь ромба равна произведению квадрата его стороны и синуса его угла. Поэтому
Ответ: 0,5. Ответ: 0,5 3. B 5 № 27767. Решение.
Ответ: 116. Ответ: 116 4. B 5 № 317337. В треугольнике ABC отрезок DE — средняя линия. Площадь треугольника CDE равна 38. Найдите площадь треугольника ABC. Решение.
Треугольник ABC подобен треугольнику DEC с коэффициентом 2. Площади подобных фигур относятся как квадрат коэффициента подобия, поэтому
Ответ: 152. Ответ: 152 5. B 5 № 27577. Решение.
Ответ: 6. Ответ: 6 B 5 № 27779.
Решение. Угол между высотами равен углу между сторонами, к которым они проведены: Ответ: 82. Ответ: 82 7. B 5 № 27729. Решение. Координаты вектора равны разности координат конца вектора и его начала. Координаты точки A вычисляются следующим образом: 5 − x = 3, 4 − y = 1. Откуда x = 2, y = 3. Поэтому сумма координат точки A равна 5.
|

 значит,
значит,
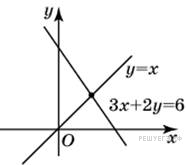 Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x.
Найдите абсциссу точки пересечения прямых, заданных уравнениями 3 x + 2 y = 6 и y = x.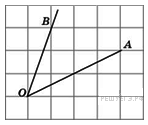 Найдите тангенс угла
Найдите тангенс угла  .
.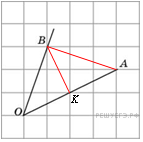 Достроим угол до треугольника
Достроим угол до треугольника 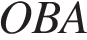 ,
,  .
.  делит основание
делит основание  пополам, значит,
пополам, значит,  .
. .
.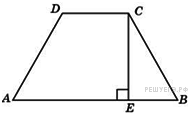 Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.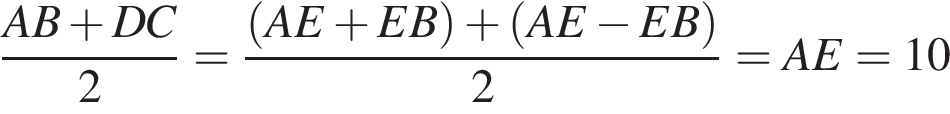 .
.
 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.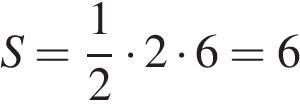 см2.
см2.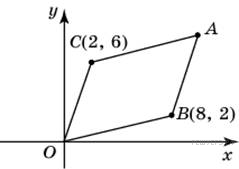 Точки O (0; 0), B (8; 2), C (2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A.
Точки O (0; 0), B (8; 2), C (2; 6) и A являются вершинами параллелограмма. Найдите ординату точки A. ,
,  ,
,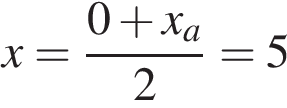 ,
,  .
. ,
, 
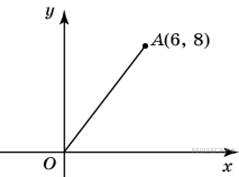 Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс.
Найдите синус угла наклона отрезка, соединяющего точки O (0; 0) и A (6; 8), с осью абсцисс. перпендикуляр на ось абсцисс, то получится прямоугольный треугольник. Длина
перпендикуляр на ось абсцисс, то получится прямоугольный треугольник. Длина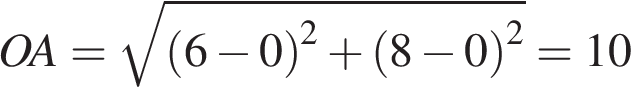 .
. .
.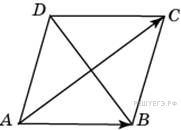 Диагонали ромба
Диагонали ромба  равны 12 и 16. Найдите длину вектора
равны 12 и 16. Найдите длину вектора 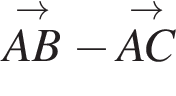 .
.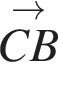 . Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Вектор
. Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Вектор 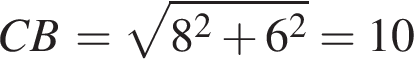 .
. На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?
На клетчатой бумаге изображён круг. Какова площадь круга, если площадь заштрихованного сектора равна 32?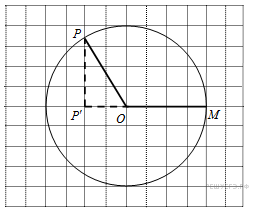 Заметим, что
Заметим, что  Тогда
Тогда 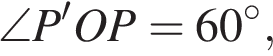 поэтому
поэтому  Поэтому площадь сектора равна
Поэтому площадь сектора равна  от площади круга. Следовательно, площадь круга равна
от площади круга. Следовательно, площадь круга равна 
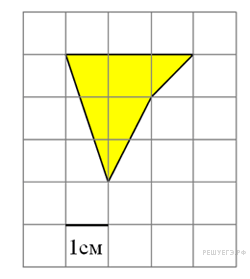 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 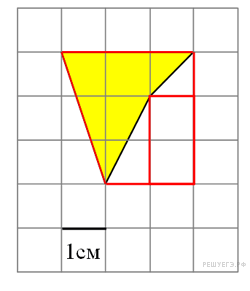 Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому см2.
см2.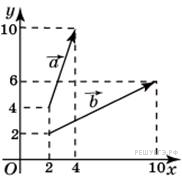 Найдите квадрат длины вектора
Найдите квадрат длины вектора 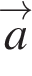 +
+ 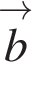 .
. , вектор
, вектор 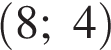 . Координаты суммы векторов равны сумме соответствующих координат. Тогда вектор
. Координаты суммы векторов равны сумме соответствующих координат. Тогда вектор  имеет координаты
имеет координаты 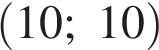 . Длина вектора
. Длина вектора  . Поэтому квадрат длины вектора равен
. Поэтому квадрат длины вектора равен  .
.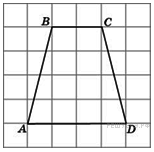 Найдите среднюю линию трапеции
Найдите среднюю линию трапеции 
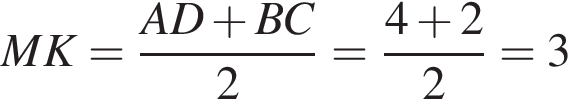 .
. Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции. см2.
см2. Найдите медиану треугольника
Найдите медиану треугольника  , проведенную из вершины
, проведенную из вершины 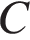 , если стороны квадратных клеток равны 1.
, если стороны квадратных клеток равны 1.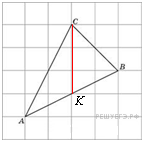 медиана проведенная из вершины
медиана проведенная из вершины 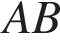 пополам. Построим отрезок
пополам. Построим отрезок  . Видно, что он равен 3.
. Видно, что он равен 3.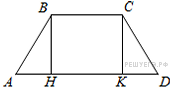 Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.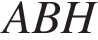 и
и 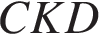 равны (
равны (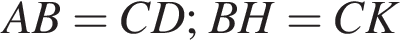 ), значит,
), значит, 

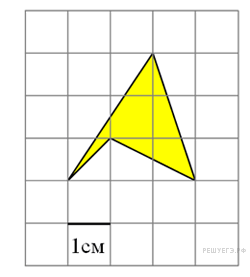 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 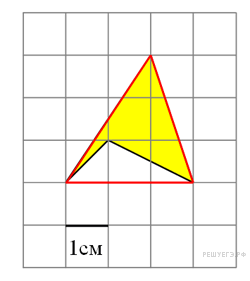 Площадь четырёхугольника равна разности площади большого треугольника и маленького треугольника. Поэтому
Площадь четырёхугольника равна разности площади большого треугольника и маленького треугольника. Поэтому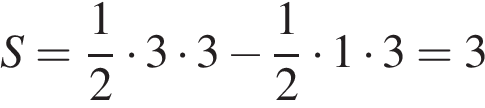
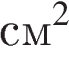 .
.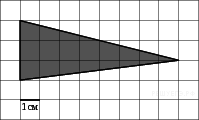 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см 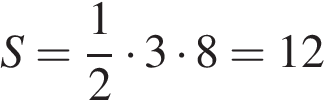 см2.
см2.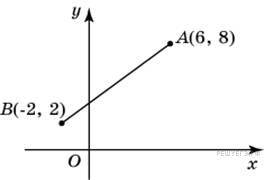 Найдите ординату середины отрезка, соединяющего точки A (6, 8) и B (-2, 2).
Найдите ординату середины отрезка, соединяющего точки A (6, 8) и B (-2, 2). ,
, 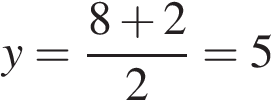 .
. В треугольнике
В треугольнике  , угол
, угол 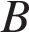 равен
равен  .
.  ,
, 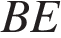 и
и  – высоты, пересекающиеся в точке
– высоты, пересекающиеся в точке  . Найдите угол
. Найдите угол 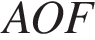 . Ответ дайте в градусах.
. Ответ дайте в градусах. .
.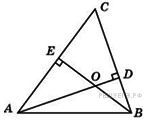 Два угла треугольника равны
Два угла треугольника равны  и
и  . Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.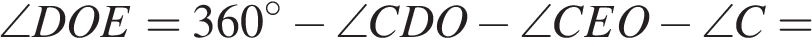
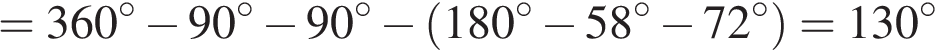 .
.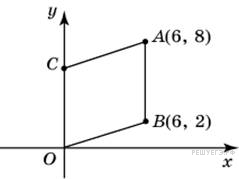 Точки O (0; 0), A (6; 8), B (6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Точки O (0; 0), A (6; 8), B (6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C. ,
,  . Известно, что
. Известно, что 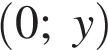 , следовательно,
, следовательно,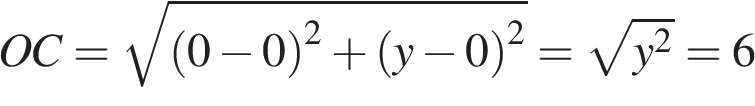 .
. .
.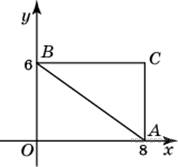 Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).
Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8; 0), (0; 6), (8; 6).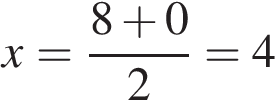 ,
,  .
.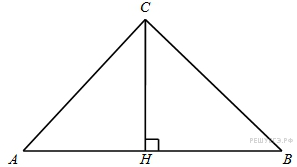 В треугольнике
В треугольнике  ,
, 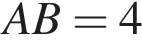 , высота
, высота  равна
равна  . Найдите угол
. Найдите угол  .
. Поскольку искомый угол ACB вдвое больше, он равен 60
Поскольку искомый угол ACB вдвое больше, он равен 60  Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны  и
и 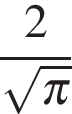 .
.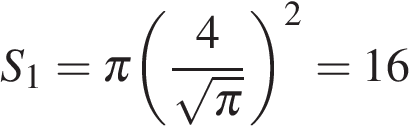 ,
, 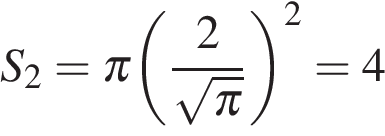 .
. .
.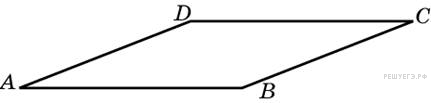 Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°.
Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°. см2.
см2.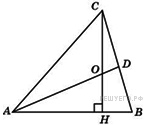 В треугольнике
В треугольнике  угол
угол  равен
равен  . Найдите угол
. Найдите угол 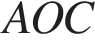 . Ответ дайте в градусах.
. Ответ дайте в градусах.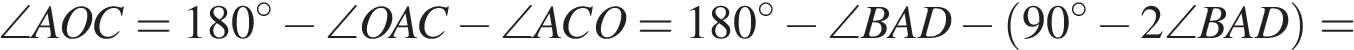
 .
.
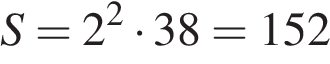 .
. Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;5), (4;7), (1;9).
Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;5), (4;7), (1;9).
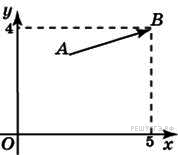 Вектор
Вектор  с концом в точке
с концом в точке 


