Решение. 41 страница
Ответ: 3. Ответ: 3 2. B 5 № 27456. Решение.
Примечание. Можно заметить и доказать, что равнобедренный треугольник ABO является прямоугольным. Тогда углы AOB и OАB равны 45°, а их тангенсы равны 1.
Ответ: 1. Ответ: 1 3. B 5 № 27670.
Решение. Прямые параллельны, поэтому их угловые коэффициенты равны. Тогда
Ответ: 9. Ответ: 9 B 5 № 27571.
Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
Ответ: 30. Ответ: 30 B 5 № 27674.
Решение. Так как у параллелограмма противоположные стороны попарно равны, то
Поэтому
Ответ: 6. Ответ: 6 6. B 5 № 27726. Вектор Решение. Пусть координаты точки B равны xB и yB. xB. Координаты вектора равны разности соответствующих координат его конца и начала. Следовательно, xB − 3 = 9, yB − 6 = 3. Откуда xB = 12, yB = 9. Поэтому сумма координат точки B равна 21.
Ответ: 21. Ответ: 21 7. B 5 № 27564. Решение. Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Ответ: 12. Ответ: 12 8. B 5 № 27925. Решение.
откуда
Ответ: 6. Приведем другое решение (Р. А., СПб.).
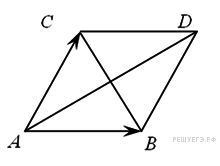
Хорды AD, DC и CB равны, поэтому равны и стягиваемые ими дуги. Вписанный угол А равен 60°, он опирается на две из этих дуг и равен половине их суммы. Поэтому каждая из дуг равна 60°, их сумма равна 180°, а хорда АВ является диаметром. Отсюда получаем, что искомый радиус равен 6. Ответ: 6 9. B 5 № 244993. Решение.
Примечание. Площадь четырёхугольника, диагонали которого перпенликулярны, равна половине произведения диагоналей. Поэтому искомая площадь равна 4. Ответ: 4 B 5 № 245004.
Вариант № 3658694 B 5 № 245006.
Решение.
Примечание. Четырёхугольник составлен из двух треугольников, имеющих общее основание, равное длине квадратной клетки: прямоугольного с катетами 1 и 1, и тупоугольного с основанием длины 1 и высотой, проведенной к этому основанию, также длины 1. Поэтому площадь четырехугольника равна 0,5 + 0,5 = 1. Ответ: 1 B 5 № 27588 . Решение. Площадь прямоугольного треугольника равна половине произведения его катетов. Пусть неизвестный катет равен a. Тогда
откуда a = 8 см. Ответ: 8. Ответ: 8 3. B 5 № 319056. Площадь параллелограмма Решение.
Четырехугольник, вершинами которого являются середины сторон произвольного четырехугольника, является параллелограммом, площадь которого равна половине площади исходного четырехугольника (см. параллелограмм Вариньона).
Поэтому его площадь равна 76,5.
Ответ:76,5. Ответ: 76,5 4. B 5 № 27948. Решение. радиус окружности, вписанной в квадрат, равен половине его стороны.
Ответ: 2. Ответ: 2 5. B 5 № 27716. Решение. Разность векторов
Ответ: 10. Ответ: 10 B 5 № 55603.
Решение. Пусть радиус окружности равен R, тогда площадь круга определяется формулой S = πR2, длина окружности определяется формулой l = 2πR. Поэтому
Ответ: 42. Ответ: 42 7. B 5 № 244983.
Решение.
Примечание. Наш четырёхугольник — ромб, его площадь равна половине произведения диагоналей. Поэтому она равна 3. Ответ: 3 8. B 5 № 27747. Решение. так как треугольник
Ответ: 64. Ответ: 64 9. B 5 № 27896. Решение. вписанный угол опирающийся на диаметр окружности, является прямым, значит,
Ответ: 6. Ответ: 6 B 5 № 27605.
Вариант № 3658804 1. B 5 № 27658. Решение. Координаты точки, делящей отрезок пополам, считаются по формуле:
Ответ: 5. Ответ: 5 2. B 5 № 27598. Решение. Площадь сектора круга, центральный угол которого равен
Ответ: 0,25. Ответ: 0,25 B 5 № 55603.
Решение. Пусть радиус окружности равен R, тогда площадь круга определяется формулой S = πR2, длина окружности определяется формулой l = 2πR. Поэтому
Ответ: 42. Ответ: 42 4. B 5 № 27561. Решение. Площадь параллелограмма равна произведению основания на высоту, проведенную к этому основанию или его продолжению. Поэтому
Примечание. Приведем другое решение. Площадь параллелограмма равна разности площади прямоугольника и двух равных прямоугольных треугольников, гипотенузы которых являются сторонами параллелограмма. Поэтому
Ответ: 12. Ответ: 12 5. B 5 № 27924. Решение. трапеция
Ответ: 6. Ответ: 6 6. B 5 № 244983.
Решение.
Примечание. Наш четырёхугольник — ромб, его площадь равна половине произведения диагоналей. Поэтому она равна 3. Ответ: 3 7. B 5 № 27679. Решение. Пусть точка P является серединой отрезков OA и BC. Координаты точки P вычисляются следующим образом:
но с другой стороны,
Поэтому
Ответ: 2. Ответ: 2 8. B 5 № 27720. Решение.
Ответ: 6. Ответ: 6 9. B 5 № 27572. Решение. Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
Ответ: 9. Ответ: 9 10. B 5 № 244995.
Решение.
Примечание. Отрезав от фигуры верхний правый прямоугольный треугольник с катетами 1 и 2, можно приложить его к левому нижнему прямоугольному треугольнику, достроив тем самым фигуру до прямоугольника со сторонами 1 и 3, площадь которого равна 3. Ответ: 3 Решение. Периметр прямоугольника равен сумме длин его сторон. Площадь прямоугольника равна произведению его длины на ширину. Пусть одна из сторон прямоугольника равна a, вторая равна b. Периметр прямоугольника будет соответственно равен P = 2
Тем самым, S = a · b = 48.
Ответ: 48. Ответ: 48 Решение.
Примечание. Заданный четырёхугольник можно рассматривать как два прямоугольных треугольника с катетами 1 и 2, которые, приложив их гипотенузы друг к другу, можно сложить в прямоугольник со сторонами 1 и 2, площадь которого равна 2. Ответ: 2 Решение. Диагональ прямоугольника образует два прямоугольных треугольника. Диагональ равна диаметру окружности, описанной около треугольника, следовательно, центр окружности лежит на середине диагонали прямоугольника. Тогда можно легко найти координаты центра окружности.
Ответ: 1. Ответ: 1 Решение.
Ответ: -2.
Ответ: -2
Вариант № 3658954 1. B 6 № 320199. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание.
|

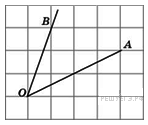 Найдите тангенс угла
Найдите тангенс угла  .
.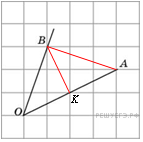 Достроим угол до треугольника
Достроим угол до треугольника  ,
,  .
.  делит основание
делит основание  пополам, значит,
пополам, значит,  .
. .
.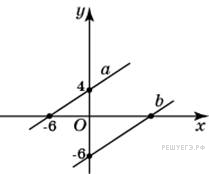 Прямая a проходит через точки с координатами (0; 4) и (−6; 0). Прямая b проходит через точку с координатами (0; −6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью O
Прямая a проходит через точки с координатами (0; 4) и (−6; 0). Прямая b проходит через точку с координатами (0; −6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью O , откуда
, откуда  .
. Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6).
Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6). см2.
см2.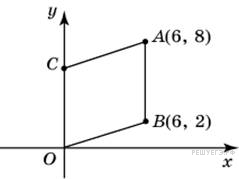 Точки O (0; 0), A (6; 8), B (6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C.
Точки O (0; 0), A (6; 8), B (6; 2) и C являются вершинами параллелограмма. Найдите ординату точки C. ,
,  . Известно, что
. Известно, что 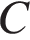 имеет координаты
имеет координаты 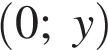 , следовательно,
, следовательно,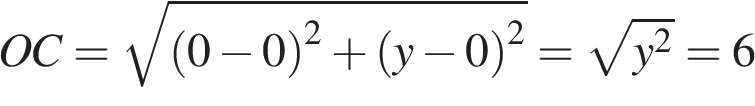 .
. .
.
 с началом в точке
с началом в точке  (3; 6) имеет координаты (9; 3). Найдите сумму координат точки
(3; 6) имеет координаты (9; 3). Найдите сумму координат точки 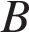 .
. Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).
Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9).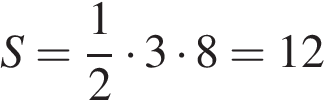 см2.
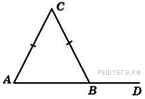
см2. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции. Окружность, описанная вокруг трапеции, описана и вокруг треугольника
Окружность, описанная вокруг трапеции, описана и вокруг треугольника 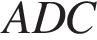 . Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:
. Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:
 Тогда по теореме синусов:
Тогда по теореме синусов:
 Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах
1 см (см. рис.). Ответ дайте в квадратных сантиметрах Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких прямоугольников и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких прямоугольников и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому 
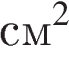 .
. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Площадь четырёхугольника равна разности площади трапеции, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
 Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет. см2,
см2, равна 153. Найдите площадь параллелограмма
равна 153. Найдите площадь параллелограмма  , вершинами которого являются середины сторон данного параллелограмма.
, вершинами которого являются середины сторон данного параллелограмма.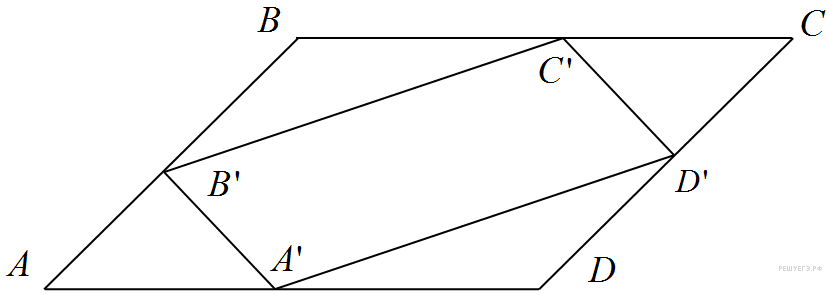
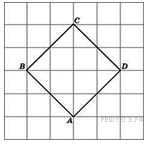 Найдите радиус окружности, вписанной в квадрат
Найдите радиус окружности, вписанной в квадрат  .
.
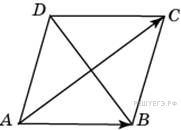 Диагонали ромба
Диагонали ромба 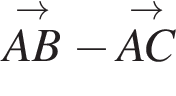 .
.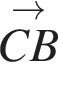 . Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Вектор
. Диагонали ромба перпендикулярны и точкой пересечения делятся пополам. Вектор 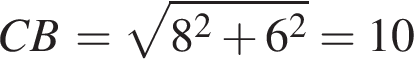 .
. Площадь круга равна
Площадь круга равна  . Найдите длину его окружности.
. Найдите длину его окружности. ,
,  , значит,
, значит, 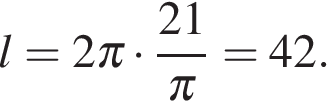
 Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см  Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких квадратов и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь четырёхугольника равна разности площади большого квадрата, двух маленьких квадратов и четырёх прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
 В треугольнике
В треугольнике 
 . Внешний угол при вершине
. Внешний угол при вершине  . Найдите угол
. Найдите угол  .
. Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.
Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника. – диаметр.
– диаметр.
 Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.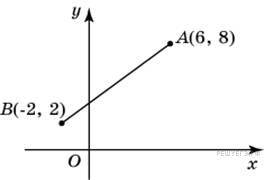 Найдите ординату середины отрезка, соединяющего точки A (6, 8) и B (-2, 2).
Найдите ординату середины отрезка, соединяющего точки A (6, 8) и B (-2, 2). ,
, 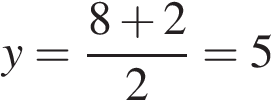 .
. Найдите площадь сектора круга радиуса
Найдите площадь сектора круга радиуса  , центральный угол которого равен 90°.
, центральный угол которого равен 90°. n° равна четверти площади круга. Поэтому
n° равна четверти площади круга. Поэтому .
. На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  см2.
см2. см2.
см2. Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.
Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.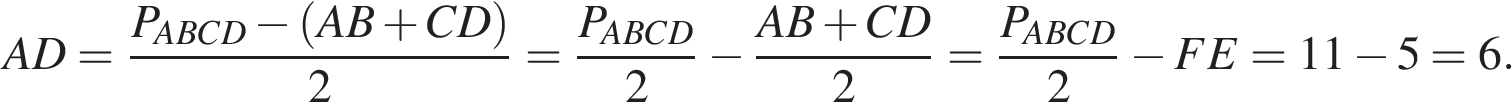
 Точки O (0; 0), A (10; 8), B (8; 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.
Точки O (0; 0), A (10; 8), B (8; 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.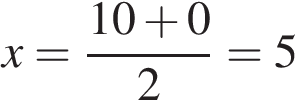 ,
, 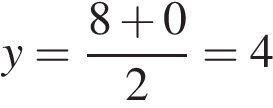 ,
,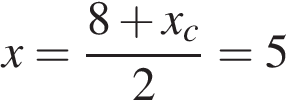 ,
,  .
. ,
, 
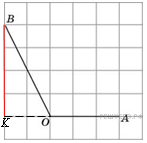
 Стороны правильного треугольника
Стороны правильного треугольника  . Найдите длину вектора
. Найдите длину вектора  .
. Достраиваем треугольник до ромба. Поскольку
Достраиваем треугольник до ромба. Поскольку  необходимо найти длину большей диагонали ромба, равную удвоенной длине медианы равностороннего треугольника. Таким образом, имеем:
необходимо найти длину большей диагонали ромба, равную удвоенной длине медианы равностороннего треугольника. Таким образом, имеем: .
. Найдите площадь трапеции, изображенной на рисунке.
Найдите площадь трапеции, изображенной на рисунке. см2.
см2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  Площадь четырехугольника равна разности площади большого прямоугольника и двух одинаковых треугольников, площади которых равны половине произведения основания на высоту, проведенную к этому основанию. Поэтому
Площадь четырехугольника равна разности площади большого прямоугольника и двух одинаковых треугольников, площади которых равны половине произведения основания на высоту, проведенную к этому основанию. Поэтому
 a + 2
a + 2 
 Площадь четырёхугольника равна разности площади большого прямоугольника, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому
Площадь четырёхугольника равна разности площади большого прямоугольника, маленького прямоугольника и двух прямоугольных треугольников, гипотенузы которых являются сторонами исходного четырёхугольника. Поэтому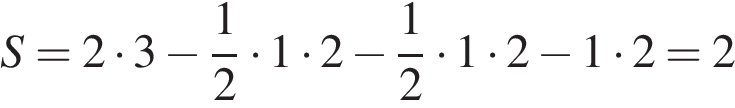
 ,
,  .
. проведем высоту
проведем высоту  .
.


