Критерии оптимальности экономико-математической модели
Тщательная подготовка и математическая формулировка экономико-математическойзадачи требует не только обоснования системы переменных и ограничений, но и грамотного выбора критерия оптимальности. При математическом моделировании выделяют глобальный и локальные критерии оптимальности. Глобальный критерий оптимальности – это критерий функционирования народного хозяйства как целостной экономической системы. Он должен максимизировать благосостояние общества и направлен на максимум совокупного общественного продукта, национального дохода, фонда накопления, фонда потребления и т.д. Процессы, направленные на решение частных экономико-математических задач в АПК, преследуют конкретные цели и оптимизируются с помощью локальных критериев оптимальности. Их особенность в том, что каждый локальный критерий не должен противоречить требованиям глобального и при этом более полно учитывать особенность решаемой задачи. Подобный подход правомерен, так как в рамках народного хозяйства имеются комплексы, отрасли, формирования, организации, которые имеют свои специфические цели и задачи. Разработка любой прогнозной оптимизационной модели требует того, чтобы в ней задавалось достижение экстремального (максимального или минимального) значения какого-то экономического результата в виде конкретной математической функции. В связи с этим количественным выражением критерия оптимальности (т.е. его отражением в аналитической форме) будет являться целевая функция. Для сельскохозяйственного производства существует множество частных задач: по оптимизации трансформации угодий, проектированию севооборотов, планированию структуры посевов и т.д. В этих случаях в качестве критериев оптимальности используются простейшие показатели оценки экономической эффективности. Но поскольку сельское хозяйство многокритериальное по своему характеру, то в качестве целевых функций для различных экономико-математических задач могут применяться многообразные локальные критерии: – максимизирующие прибыль, валовой и чистый доход, валовую и товарную продукцию, рентабельность, производительность труда и др.; – минимизирующие издержки производства, приведенные затраты, некоторые виды ресурсов (пашни, кормов), затрат труда. Целевые функции могут быть представлены в стоимостном или натуральном исчислении. В качестве примера последних можно привести такие: минимум расхода горюче-смазочных материалов, максимум накопления в почве органического вещества, минимум коэффициента эрозионной опасности культур. В общем виде целевая функция линейной оптимизационной задачи записывается следующим образом:
где Многие задачи предполагают вычисление целевой функции в процессе решения. Допустим, значение прибыли может рассчитываться так:
где
Таким образом, первая часть функционала представляет собой объем денежной выручки, вторая – производственные затраты реализуемой продукции, а все вместе – прибыль, которая и максимизируется. Известно, что решение конкретной задачи прогнозного развития требует обеспечения получения максимального количества выручки и прибыли, снижения издержек производства, роста производительности труда и т.д., т.е. ее качество оценивается по многим показателям. Однако оптимальные проектные решения, получаемые в результате использования разных критериев при постановке одной задачи, могут существенно отличаться. Возможна ситуация, когда план, максимизирующий объемы товарной продукции в стоимостном выражении, может привести к высоким издержкам производства, и в результате, к снижению чистого дохода. В то же время план, минимизирующий объем трудовых затрат на производство продукции, может значительно снизить объем валовой продукции или выручки. В связи с этим возникает проблема поиска такого решения, которое было бы наилучшим с учетом всех критериев оптимальности (его чаще всего называют компромиссным). Для реализации такого подхода необходимо: а) обосновать перечень критериев, подлежащих рассмотрению в конкретной задаче. Он устанавливается на основе логического анализа, обычно одновременно стараются учесть не более трех или четырех критериев; б) дать оценку относительной предпочтительности критериев. Она может быть проведена на основе метода экспертных оценок. При невозможности установить шкалу предпочтительности исходят из предположения экономической равнозначности каждого критерия; в) выбор схемы компромисса. Разработаны различные методы нахождения компромиссных решений. Наиболее простой и практически реализуемый – метод последовательных уступок. Сначала ранжируют критерии по их важности. Затем одну и ту же задачу решают по каждому из выбранных критериев, начиная с менее важного. Допустим из четырех критериев были получены три варианта ЭМЗ. После этого решается задача по последнему, наиболее важному критерию, где полученные ранее значения трех критериев входят в качестве ограничений (на уровне более низком, чем рассчитанные оптимальные параметры каждого критерия). Метод штрафных функций заключается в том, что к основному критерию прибавляются некоторые специальные функции, сформулированные по остальным критериям. Эти так называемые штрафные функции ухудшают значение функционала на столько, на сколько отклоняются от своих экстремальных значений учитываемые ими показатели. Решив задачу по новому критерию, получаем компромиссный план. Метод равных и наименьших относительных отклонений разработан польским ученым И. Ныковским. Его суть состоит в том, что исходная задача решается по каждому критерию отдельно. После этого ставится требование, чтобы компромиссному плану соответствовали равные и минимальные относительные отклонения всех критериев от своих экстремальных значений. Равенство отклонений обеспечивается дополнительными ограничениями, вводимыми в задачу, а минимизация – новой целевой функцией. Предпочтительность критериев можно учесть путем введения поправочных коэффициентов. Чешским ученым И. Саской разработан метод линейного мультипрограммирования. Содержание его состоит в том, что после отыскания оптимума для каждого рассматриваемого критерия в многограннике решений определяется точка, максимальное удаление которой от всех гиперплоскостей, соответствующих экстремальным значениям функционалов, было бы минимально. Немецким исследователем Х. Юттлером был предложен метод выпуклой комбинации, где сначала отыскивают оптимальные планы по каждому критерию, а затем составляют их выпуклую линейную комбинацию, коэффициенты которой находят из решения дополнительной задачи. Иногда приходится рассматривать задачи с линейными ограничениями, но с нелинейной целевой функцией. В этом случае целесообразно стремиться к ее линеаризации. Наиболее простой в этом случае способ – аппроксимация криволинейной зависимости через ряд кусочно-линейных функций и получение на их основе приближенных решений. Рассматриваемые приемы получения компромиссного решения имеют как положительные, так и отрицательные стороны, в том числе и определенные условности. Чаще всего при решении конкретных экономико-математических задач, имеющих многокритериальный характер, часть возможных критериев непосредственно учитывают в ограничениях. Например, ограничение по прибыли взаимоувязывают с ограничением по использованию капвложений и формированию фондов, а в качестве целевой функции выступает максимизация стоимости конечной продукции за вычетом той ее части, которая направляется на погашение кредитных средств. При такой постановке получается компромиссный вариант, по которому будет предложен план с возможно большой прибылью, меньшей фондоемкостью отраслей, наивысшим вложением собственных инвестиций в развитие производства и максимальной денежной выручкой.
|

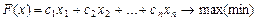 или же
или же 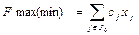 ,
,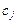 – рассчитанные коэффициенты целевой функции (например, стоимость товарной продукции в расчете на 1 га или 1 голову. Тогда находится максимум реализуемой товарной продукции в стоимостном выражении).
– рассчитанные коэффициенты целевой функции (например, стоимость товарной продукции в расчете на 1 га или 1 голову. Тогда находится максимум реализуемой товарной продукции в стоимостном выражении).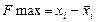 ,
,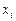 – суммарная денежная выручка (финансовый ресурс i), вычисляемая в процессе решения задачи, исходя из имеющегося ограничения
– суммарная денежная выручка (финансовый ресурс i), вычисляемая в процессе решения задачи, исходя из имеющегося ограничения 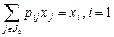 ; здесь
; здесь 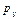 – выручка (ресурс i) от реализации единицы продукции вида j;
– выручка (ресурс i) от реализации единицы продукции вида j; – суммарная себестоимость (ресурс i) реализуемой продукции, вычисляемая в процессе решения задачи, исходя из имеющегося ограничения
– суммарная себестоимость (ресурс i) реализуемой продукции, вычисляемая в процессе решения задачи, исходя из имеющегося ограничения 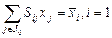 ; здесь
; здесь 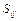 – издержки (ресурс i) на единицу реализуемой продукции вида j.
– издержки (ресурс i) на единицу реализуемой продукции вида j.


