Пересечение тел вращения проецирующей плоскостью

 

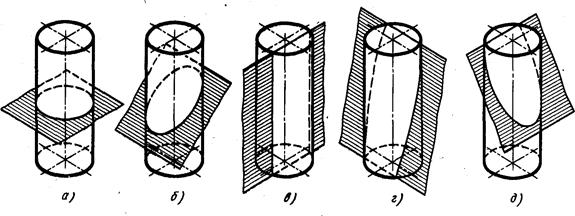
При пересечении тела вращения плоскостью контур пересечения будет представлять собой замкнутую кривую линию, форма которой зависит от формы тела вращения и положения секущей плоскости относительно оси вращения. Это может быть окружность, эллипс, парабола, гипербола, а также различные сложные сочета­ния кривых линий. Чтобы построить линию пересечения поверхности вращения с секущей плоскостью, необходимо построить ряд точек, которые будут принадлежать и поверхности тела вращения, и плоскости. Построение следу­ет начинать с характерных точек. К таким точкам относятся: габаритные точки, опреде­ляющие наибольшие размеры линии пересече­ния по высоте и ширине; точки, лежащие на крайних образующих и образующих, проекции которых совпадают с 'осевыми линиями. По расположению этих точек можно представить характер искомой линии пересечения.

Построив характерные точки, строят проме­жуточные точки, используя для этого в качест­ве вспомогательных линий прямые - образую­щие или окружности (меридианы и паралле­ли). Строя линию пересечения, необходимо знать, по какой кривой пересекаются тела вра­щения - цилиндр, конус, шар и тор.

Пересечение цилиндра проецирующей плоскостью. Если прямой круговой цилиндр рассечь плос­костью, параллельной его основаниям, то линия пересечения боковой поверхности с этой плоскостью будет окружность (рис. 4, а).

 

 

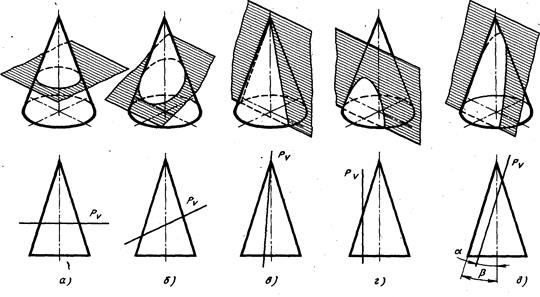
Рис. 4

Если цилиндр рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности с этой плоскостью будет эллипсом, величина и форма которого зависят от угла наклона секу­щей плоскости к плоскостям оснований ци­линдра (рис.4, б).

Если цилиндр рассечь плоскостью, перпенди­кулярной к его основаниям, линия пересечения боковой поверхности с этой плоскостью будет прямоугольником (рис. 4, в).

Если цилиндр рассечь наклонной плоско­стью так, что она пересечет основания и бо­ковую поверхность, то линия пересечения бу­дет частью эллипса, отсеченной двумя хордами оснований (рис. 4, г).

Если секущая плоскость пересечет одно ос­нование и часть боковой поверхности, то ли­ния пересечения боковой поверхности с этой плоскостью будет частью эллипса отсеченного одной хордой основания (рис.4, д).

Пересечение цилиндра проецирующей плоскостью и построения сечения приведен на рис. В4 Вначале построили опорные точки A,B (наивысшая и самая низкая) и C,D (определяют границу видимости). Все остальные точки промежуточные, построены исходя из свойства принадлежности точки линии. Для их нахождения использовались горизонтали (дополнитель­ные образующие). На рис.В4 проведено 12 образующих. Для этого на профильной проек­ции, проекцию основания цилиндра делят на 12 равных частей и через точки деления строят фронтальные и горизонтальные проекции этих образующих. Прежде чем начать построение линии среза, надо представить себе эту ли­нию.

Развертка поверхности усеченного цилиндра. При построении развертки поверхности усе­ченного цилиндра сначала строят развертку боковой поверхности полного цилиндра, кото­рая представляет собой прямоугольник. Высота прямоугольника равна высоте цилиндра (в данном случае длине образующей, рис. B5). Длина пря­моугольника строится приближенно. Для этого на профильной проекции измеряют хорду между двумя любыми соседними точками деления ок­ружности основания и откладывают это рас­стояние 12 раз по нижней стороне развертки боковой поверхности цилиндра. Затем из всех полученных точек проводят образующие, на которых от нижней части развертки вверх от­кладывают расстояния, равные длинам усечен­ных образующих, взятых с фронтальной или горизонтальной проекций. Построенные на развертке боко­вой поверхности цилиндра точки соединяют от руки плавной кривой линией и обводят по лека­лу. Далее пристраивают полное основание к любой образующей боковой поверхности снизу, а сверху - часть основания, оставшуюся после рассечения цилиндра плоскостью, и натураль­ную величину среза.Развертка поверхности усеченного цилиндра приведена на рис. В5.

Пересечение конуса проецирующей плоскостью. На рис. 5 показаны примеры пересечения конуса плоскостями различного положения, где каждому наглядному изображению соответствует фронтальная проекция конуса со следом секущей плоскости.

Если прямой круговой конус рассечь плоско­стью, параллельной основанию, то линия пере­сечения боковой поверхности конуса с плоско­стью будет окружностью (рис. 5, а).

Если конус рассечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности конуса с плоскостью будет эллипсом (рис. 5, б ).

Если конус рассечь плоскостью, проходящей через его вершину, то, будет ли плоскость пер­пендикулярна или наклонна к основанию, линия пересечения боковой поверхности конуса с пло­скостью будет треугольником (рис. 5, в ).

Рис. 5

 

Если на поверхности конуса можно провести две образующие параллельно пересекающей его плоскости, то такая плоскость пересечет боко­вую поверхность конуса по гиперболе (рис. 5, г ).

Если плоскость пересекает конус параллельно одной образующей, то боковая поверхность конуса пересечется этой плоскостью по парабо­ле (рис. 5, д ).

Пересечение шара проецирующей плоскостью. Шар представляет собой единственное гео­метрическое тело, поверхность которого пересе­кается плоскостью любого положения всегда по окружности.

Секущие плоскости, проходящие через верти­кальную ось шара, рассекают его по меридианам. Секущие плоскости, проходящие перпен­дикулярно к вертикальной оси шара, рассекают его по параллелям.

Пересечение тора проецирующей плоскостью. Если тор пересекать плоскостями, проходя­щими через ось тора, то линия пересечения по­верхности тора и плоскости в зависимости от формы образующей тора, будет либо окруж­ностью, либо дугой окружности.

Если тор пересекать плоскостями, перпенди­кулярными оси вращения, то его поверхность будет пересекаться всегда по окружности.

Если тор пересекать плоскостями, наклонны­ми к оси вращения или параллельно ей, то его поверхность будет пересекаться по кривым ли­ниям.

Еще раз обратим внимание на то что изображено на рисунках приложения В:

- рисунок В4- образец выполнение эпюра 3(построение сечения цилиндра);

- рисунок В5- образец выполнение эпюра 3(построение развертки цилиндра);

- рисунок В6- образец выполнение эпюра 3(построение сечения призмы);

- рисунок В. 7- образец выполнение эпюра 3 (построение развертки призмы).

 

Контрольные вопросы при защите РГР 3

1 Чем можно задать поверхности вращения?

2 Как образуются поверхности вращения: сфера, тор, конус, цилиндр?

3 Какие линии на поверхности вращения называются параллелями и меридианами?

4 Как образуются цилиндрическая и коническая поверхности общего вида?

5 Как построить проекции произвольной точки, принадлежащей заданной поверхности?

6 Какие линии получаются при сечении прямого кругового цилиндра плоскостью?

7 Какие линии получаются при сечении конуса плоскостью?

8 Какие линии получаются при сечении сферы плоскостью и какими могут быть проекции этих линий?

9 Чему равна малая ось эллипса при сечении прямого кругового цилиндра плоскостью?

10 Как определить малую ось эллипса при сечении кругового конуса проецирующей плоскостью?

11 Какими способами можно найти натуральную величину сечения тела плоскостью?

12 Какое сечение цилиндра называется нормальным?

13 Каков алгоритм нахождения точек пересечения прямой с поверхностью?

14 Какие вспомогательные плоскости применяются при определении точек пересечения прямой и поверхности?

15 Как определяется видимость точек пересечения прямой с поверхностью геометрических тел различного вида?

16 В чем заключается способ посредников при построении точек, общих для двух пересекающихся поверхностей?

17 Как построить развертку поверхности конуса?

18 Как построить развертку поверхности цилиндра?

17 Как построить развертку поверхности пирамиды?

18 Как построить развертку поверхности призмы?