Метод концентрических сфер
Задача. Построить линию пересечения двух поверхностей вращения: конуса (Ф1) и цилиндра (Ф2). Графическое оформление задачи приведено на рис. 8. Метод концентрических сфер применяется при одновременном выполнении трех условий: 1) пересекающиеся поверхности должны быть поверхностями вращения; 2) оси поверхностей должны пересекаться; 3) поверхности должны иметь общую плоскость симметрии, параллельную одной из плоскостей проекций. Анализ и решение задачи:
Рис.8
Первый шаг алгоритма записываем аналогично методу плоских посредников: 1) где точка 1 – верхняя, точка Для нахождения остальных точек, принадлежащих искомой линии, вводим сферические посредники. Сферические посредники должны проводиться из точки пересечения осей поверхностей, поскольку только в этом случае они (посредники) окажутся соосными с каждой из пересекающихся поверхностей. В качестве минимального посредника должна приниматься большая из сфер - Р 2, вписанных из точки пересечения осей (i и ј) в каждую поверхность в отдельности. Это связано с тем, что меньшая из вписанных сфер - Р 0 не дает линии пересечения (или касания) с другой поверхностью (Φ1) и, следовательно, не дает точки, общей для пересекающихся поверхностей. В качестве максимального посредника принимается сфера (Р 1), радиус которой равен расстоянию от точки пересечения осей i и ј до наиболее удаленной точки ( Записываем второй шаг алгоритма: 2) Р 2 > Р 0; Р 2 ∩ Φ1 = m 2; Р 2 ∩ Φ2 = n 2; m 2 ∩ n 2 = Остальные сферические посредники должны быть радиусом больше принятого минимального посредника Р 2 и меньше максимального посредника Р 1. Для определения границы зоны видимости горизонтальной проекции искомой линии ℓ; через условный экватор цилиндра Φ2 (через ось j) проводим горизонтальную плоскость уровня Записываем третий шаг алгоритма: 3) Все найденные точки являются опорными. Далее следует перейти к построению произвольных точек. Проводим сферический посредник Р 4, больший P 2 и меньший Р 1 (проекция Аналогично решается и записывается пятый шаг алгоритма: 5) Р 1 > Р 5 > Р 2; Р 5 ∩ Φ1 = m 5; Р 5 ∩ Φ2 = n 5; m 5 ∩ n 5 = 5, И заключительный шаг алгоритма: ℓ; = Образец выполнения эпюра 4 приведен в приложение Г. Контрольные вопросы при защите РГР 4 1 Чем можно задать поверхности вращения? 2 Как образуются поверхности вращения: сфера, тор, конус, цилиндр? 3 Какие линии на поверхности вращения называются параллелями и меридианами? 4 Как образуются цилиндрическая и коническая поверхности общего вида? 5 Как построить проекции произвольной точки, принадлежащей заданной поверхности? 6 Какие линии получаются при сечении прямого кругового цилиндра плоскостью? 7 Какие линии получаются при сечении конуса плоскостью? 8 Какие линии получаются при сечении сферы плоскостью и какими могут быть проекции этих линий? 9 Чему равна малая ось эллипса при сечении прямого кругового цилиндра плоскостью? 10 Как определить малую ось эллипса при сечении кругового конуса проецирующей плоскостью? 11 26 Как построить развертку сферы? 12 Какое сечение цилиндра называется нормальным? 13 Каков алгоритм нахождения точек пересечения прямой с поверхностью? 14 Какие вспомогательные плоскости применяются при определении точек пересечения прямой и поверхности? 15 Как определяется видимость точек пересечения прямой с поверхностью геометрических тел различного вида? 16 В чем заключается способ посредников при построении точек, общих для двух пересекающихся поверхностей? 17 Какие геометрические объекты могут быть использованы в качестве посредников? 18 Каков основной принцип выбора посредника? 19 По каким линиям пересекаются поверхности вращения, имеющие общую ось? 20 В каких случаях возможно и целесообразно применение способа концентрических сфер? 21 Как выбирается наименьший и наибольший радиусы концентрических сфер-посредников? 22 Какие участки линии пересечения поверхностей на чертеже будут видимыми? 23 Когда два цилиндра пересекаются по плоской кривой? 24 Как построить развертку поверхности конуса? 25 Как построить развертку поверхности цилиндра?
|
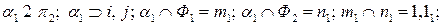
- нижняя.
), вписанные соответственно в поверхности Φ2 и Φ1 (проекции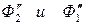 
). В качестве минимального посредника принимаем сферу Р 2 (проекция 
), отвергая Р 0 (проекция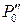 
). Через точки касания сферы Р 2 (проекция 
) проводим линию m 2 (проекции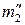 
) касания (напомним, что касание – есть частный случай пересечения) ее с конусом Φ1 (проекции 
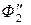) – линию n 2 (проекция 
) пересечения посредника Р 2 с цилиндром Φ2. Находим точки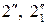 
пересечения линий в пространстве – (окружностей) 
.
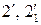- левые точки. В качестве максимального посредника принимаем сферу Р 1 (проекция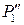 
), проходящую через ранее полученную точку 
).
(след-проекция 
). Эта плоскость 
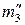), а цилиндр Φ2 по прямоугольнику, фронтальная проекция которого есть прямая 
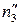, а горизонтальная проекция 
совпадает с горизонтальным очерком 
цилиндра Φ2. Горизонтальные проекции 
и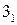 
(проекци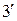и 
и 
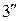). Фронтальные проекции 
и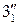 
этих точек находятся на следе-проекции 
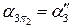плоскости 
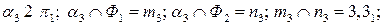- точки, определяющие границы видимости для горизонтальной плоскости проекций, одновременно являющиеся ближней и дальней точками.
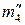). Находим фронтальные проекции 
и 
линий m 4 и n 4 пересечения посредника Р 4 с поверхностями конуса и цилиндра и точки 
параллели m 4 и на ней по линии связи – горизонтальные проекции 
искомых точек. Записываем четвертый шаг алгоритма: 4) Р 1 > Р 4 > Р 2; Р 4 ∩ Φ1 = m 4; Р 4 ∩ Р 2 = n 4; m 4 ∩ n 4 = 4, 
.
.
.
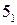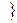