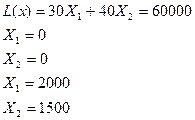Задача оптимизации доходов.
Завод изготавливает детали для автомобиля. Выпуск второго типа деталей (X1,X2). Завод располагает фондом рабочего времени 4000 ч/ч в неделю. Для производства одной детали типа X1 требуется 1 ч/ч, и для X2 2ч/ч. Производственная мощность завода позволяет выпускать X=2250 и X=1550 деталей в неделю. Каждая деталь типа X2 требуют 2 кг металлических стержней, и 5 кг листового метала. Для производства X1 (1 деталь) необходимо 5 кг стержней и 2 кг листового металла. Уровень запаса каждого вида металла составляет 10000кг. Ежедневно завод поставляет 600 деталей 1 вида своему заказчику. Существует также профсоюзное соглашение в соответствие, с которым общее число производимых в неделю деталей составляет не менее 1500штук. Требуется определить сколько деталей каждого типа нужно производить, чтобы максимизировать общий доход за неделю, если доход за неделю X1=30 у.е., X2=40 у.е.?
Критерий максимум доход, целевая функция имеет вид:
 Формализация задачи: пусть переменная
Тогда целевая функция будет иметь вид:
5
(2)
1 Д
1 2 3 4 5 6 7 8
Построение областей ограничения
Строим целевую функцию (произвольно)
Оптимальная точка определения плана производства достигается максимальным доходом. Это точка Д (1500, 1250) Аналитический способ:
Резюме Рассмотренный выше задачи оптимизации планирования производства по критерию максимум прибыли и дохода, при решения графическим или аналитическим методом, в случаи небольшой размерности переменных наглядны и точны в своих решениях.
|




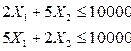




 4
4
 2 С д
2 С д