Обычно в задачах распределения однородных ресурсов имеет место многоэтапность процессов, протекающих во времени.
В методе динамического программирования имеется некоторая управляемая операция (процесс - объект), распадающаяся на m-этапов. На каждом этапе осуществляется распределение n- нераспределенных ресурсов, участвующих в операции с целью улучшения ее результатов в целом. Эти распределения ресурсов в динамическом программировании называются управлением операцией (процесс преобразования управляющего ресурса в управляющее воздействие). Эффективность операции в целом оценивается тем же показателем, что и эффективность ее управления. При этом Э(U) зависит от всей совокупности управлений на каждом этапе операции:
Закон управления, при котором показатель Задача динамического программирования всегда требует определить оптимальное управление на каждом этапе В большинстве задач, в том числе и задач распределения ресурсов требуется обеспечить:
Все вышеизложенное является постановкой задач динамического программирования в общем виде. Примечание: задача ДП как и другие задачи управления решается при наличии управленческого ресурса.
Решение задач ДП заключается в следующем алгоритме: оптимизация методом последовательных приближений, итераций в задачах ДП производится в 2 круга: в начале от последнего этапа к первому производится распределение начального ресурса от последнего этапа к первому, а затем в обратном направлении от первого к последнему. На первом круге от последнего этапа к первому находятся т.н. псевдо оптимальное управление (иногда условно оптимальное). Оно выбирается таким, чтобы все предыдущие этапы обеспечивали В общем, на каждом этапе имеется такое управление Так продолжается до первого этапа, но поскольку перед первым этапом нет предыдущего, то полученное от него псевдо оптимальное управление теряет свой псевдохарактер и становится просто начальным управлением, которое должно быть переведено в оптимальное. Второй круг оптимизации начинается с первого этапа, для которого псевдо оптимальное управление, полученное на первом круге, переводится в
где
Имея для всех этапов псевдо оптимальное управление и значения на конец каждого этапа накопленного ресурса (14.1) будем иметь оптимальное управление на каждом этапе второго круга. На этом первая итерация заканчивается. Итерационные процедуры продолжаются до тех пор, пока не будет достигнуто начальное значение начального ресурса, характеризующего возможности субъекта, проводящего операции.
Рассмотрим алгоритм ДП при решении задачи распределения однородного ресурса, имеющей следующие исходные данные: Фирма планирует совместную работу сталелитейного и автомобилестроительного заводов на трехлетний период. Начальный запас стали составляет 2300т., начальные мощности 1200т. стали и 200шт. автомобилей в год. Сталь (сырье) расходуется на производство автомобилей в количестве 4т. на 1 автомобиль на автозаводе, а на производство собственной стали на литейном заводе в соотношении 1т. затрат на 4т. выпуска. Кроме того сталь расходуется на увеличение мощности автозавода в соотношении 10т. затрат, прирост мощности 1 авто в год и на увеличение мощности сталезавода в соотношении 1т. затрат, прирост мощности сталезавода 0,15т. в год. Решение о распределении стали на следующий год принимается по показателям очередного года. Требуется о пределить мах объем выпуска продукции (авто) за весь планируемый период.
Решение сводится к построению процесса распределения начального запаса стали Этап 1: на сталезаводе Планирование выпуска объема стали, необходимого для производства авто на автозаводе, исходя из начальной собственной мощности Этап2: планирование выпуска объема стали на собственное производство определяется коэффициентом пропорциональности Этап3: планирование выпуска объема стали на увеличение мощности сталезавода
На автозаводе:планирование выпуска авто, исходя из начальной мощности завода Планирование выпуска объема авто с учетом мощности ее развития.
Согласно методу динамического программирования применительно к нашей задаче имеем 3 управления: На основании вышеизложенного алгоритма составляем исходную таблицу:
Определить псевдо оптимальное управление первого круга, начиная с третьего периода. Здесь наша задача заключается в том, чтобы найти количество стали необходимое для выпуска авто в каждом периоде.
На втором плановом периоде:
На втором круге оптимизации при определении оптимального управлений и при переходе к ним от псевдооптимальных имеем Нам необходимо для производства 280 авто на начало планового периода 850т. стали, а на конец планового периода в соответствии с количеством стали на сталезаводе, выпущенной для развития, в соответствии формулой (14.1) будем иметь оптимальное значение Определяем оптимальное управление на конец второго периода: На конец третьего периода:
-355 / 4 = 89 максимально возможный выпуск авто при таком начальном запасе без пересмотра коэффициентов и без пересмотра итерационной процедуры:280+392+548-89 =1131 авто. Если такой план выпуска авто при таком начальном ресурсе не устраивает менеджера, у него есть инструмент, который позволит ему сменить
Задача:Распределение однородных ресурсов Пусть имеются 5 видов ресурсов m=5, предназначенных для 4х объектов (этапа производственного плана) n=4. Из предыдущей практики было известно характеристики объектов и ресурсов: материальный эффект, при распределении на j объект любой единицы ресурсов Аi. Коэффициент Li характеризует возможности каждого из ресурсов применительно к конкретному объекту. Характеристики заданы в таблице 14.1.
Требуется определить количество единиц ресурса Х использование которых на каждом из объектов обеспечить. Решение: В данной задаче нет естественного разделения операций на шаге. Такое разделение введем исскуственно в соответствии с требованиями 1го пункта алгоритма. За шаги последовательное распределение ресурсов по объекту n=4. На первом шаге обозначим Х1-количество ресурсов направляемых на 4-й объект, счет шагов с конца. При этом расчет эффективности этого решения, в силу специфических особенностей задачи планирования производства, произведенных по выражению. Э1=f1(x1)=A4Pi=A4(1-e-L4X1)=2(1-е-0,1х1) 14.1 Где Рi=1-е-Li х1 В выражении 14.1 значение х1, известно т.к это количество ресурсов, которое осталось от условного оптимального U управлении на предпоследних от конца (2м от конца шаге).Переберем все возможные значения х1 и для каждого из них рассчитываем f1(х1) или Эi. Как видно из условий задачи х1 может принимать значения m=0,1,2,3,4,5. Подставляем в 14.1 значения m и после расчетов получаем:
На втором шаге (с конца) выделяется Х2 ресурсов, а соответственно Э2=f2(х2) должно учитывается по мимо эффекта от второго шага также эффект в результате условно – оптимального управления на первом с конца шага, тогда; Э2=f2(X2)=Аn-1[1-е-Ln-1(x1-x2)] 14.3 Max – ый эффект получаемый за 2 шага получается по формуле. Подставляя значения A3 и L3 в 14.2 и проведем расчеты для распределения ресурсов на втором шаге.
Таблица 14.3
В таб. 14.3, по формуле 14.2 проведены расчеты всех возможных расчетов Х2. Эффективности и одновременно определены значения Х2 зависящие от Х1 при котором f2(х2) достигает max. Далее аналогично определяем для всех возможных Х3 значения f3(Х3) и Х3(Х2). Таб 14.4
Э3=f3(Х3)=А2(1-е-L2{x3-f2(x2)}) Аналогичным путем рассчитываются условно – оптимальное на 4ом шаге с конца на первом с начала, но но на этом шаге имеется исходная начальная единица ресурсов предназначена для всех этапов, то начинается 2й круг оптимизации в обратном порядке. По сколькую в начале для всех объектов имеются 5ь единиц ресурсов m=5, а после выделения ресурсов на один из объектов в соответствии с условно – оптимальным управление Х3(Х2)=2, то тогда Х4(Х3)=3 Х4=U4=5ед-2ед=3ед. Оптимальное управлении на 3ем с конца шаге должно быть таким, что при распределении оставшихся 3х единиц ресурса выдерживался принцип оптимальности при этом Х3=2 Х1=3 Остальные 0 В этом случаи Э Резюме: Изложенный алгоритм динамического программирования применительно к задачам распределения ресурсов по этапам производственного позволяет в соответствии с принципом Басмана получить оптимальное управление по всему плану путем получения условно – оптимальных управлений на каждом из его этапов и шагов.
|


 достигает max, называется оптимальным управлением (
достигает max, называется оптимальным управлением ( ).
). , i = (1,m) и тем самым оптимальное управление в целом.
, i = (1,m) и тем самым оптимальное управление в целом. , где
, где 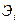 - эффективность операции на i- этапе процесса (операции).
- эффективность операции на i- этапе процесса (операции). этапа.
этапа. , которое обеспечивает псевдо оптимальное продолжение операции на
, которое обеспечивает псевдо оптимальное продолжение операции на  этапе, этот принцип выбора управления называется принципом оптимальности Беллмана.
этапе, этот принцип выбора управления называется принципом оптимальности Беллмана. путем вычитания из
путем вычитания из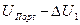 (псевдо оптимум), (14.1)
(псевдо оптимум), (14.1) - разница между начальным значением ресурса
- разница между начальным значением ресурса  на начало года и конечным значением ресурса на конец года.
на начало года и конечным значением ресурса на конец года. т. по трем потребителям: автозавод на развитие, сталезавод на развитие, сталезавод на собственное производство в течение трех плановых лет. Процесс максимизации выпуска авто складывается из следующих этапов, последовательно протекающих во времени и отражающих реальный процесс.
т. по трем потребителям: автозавод на развитие, сталезавод на развитие, сталезавод на собственное производство в течение трех плановых лет. Процесс максимизации выпуска авто складывается из следующих этапов, последовательно протекающих во времени и отражающих реальный процесс. при наличии начального запаса
при наличии начального запаса  =1200т.,
=1200т., 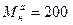 шт.
шт. равным 1т. затрат на 4т. выпуска = 0,25
равным 1т. затрат на 4т. выпуска = 0,25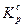 = 0,15т. к 1т. затрат.
= 0,15т. к 1т. затрат. .
. = 4т./10т. затрат =0,4
= 4т./10т. затрат =0,4 в каждом плановом периоде соответственно.
в каждом плановом периоде соответственно.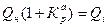
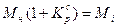

 1220 4792 6100
1220 4792 6100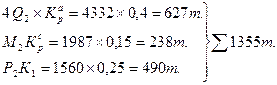

 На первом плановом периоде:
На первом плановом периоде:
 =850т.
=850т.






