В транспортных задачах.
В транспортных задачах обычно имеется база А располагающих каким-либо количеством машин n и объекты (потребители) Б нуждающихся в этих машинах, количество потребляемых машин объектами Б (m). Машины объектам Б нужны для выполнения запланированного объема работ. База А и объекты Б заинтересованы в обеспечении min простоя машин которые зависят от плана распределения их по базам и объектам. В ЛП потенциалами являются некоторые числа UAi и UБj соответственно к базам и объектам. Сумма которых для клеток табличного плана содержащих цифры распределенных машин, применяется равным результатов времени простоев:
UАi+UБj=Cij (12.1)
Там где в клетках табличного плана нет распределения машин по объектам эта сумма будет не более стоимости результатов (Cij*Хij) UАi+UБj План распределения машин по объектам отображенный в таблице планов всей клетки которого отвечают условиям 12.1, 12.2 являются оптимальными. Задача: транспортная и РУР для ее решения. Описание реального объекта. Пусть имеются предприятия занимающихся механизацией трудоемких работ и располагает набором однородных технических средств в количестве n=30 еденицам. Машины размещаются на 3х базах Реутово (А1), Железнодорожный, (А2) Балашиха, (А3) при этом базы А1и А2 имеют по 11 машин, а база А3 8ед. Использование этой техники планируется на 4х объектах Б1,Б2,Б3,Б4. Объекты Б1 нуждаются в 5ед. Б2 и Б3 нуждаются в 9ед. Б4 нуждается в 7ед. Эффективность эксплуатации max средств во многом зависит от того на сколько интенсивно они используются или не используются простаивают. При этом чем меньше время простоев, тем выше эффективность технических средств. Под простоем здесь понимается количество свободного времени (Тij) в течение которого ТС базой Аi не используются объектом Бj. Общая характеристика использования ТС с указанием ее наличия и потребности на объектах и базах приведено в таблице 12.1
Требуется разработать такой план распределения ТС по объектам, при котором суммарное время простоев ТС будет минимальным. Последовательность действий выбора наилучшей альтернативы методом потенциалов. * составляем исходный план распределения машин по следующим правилам: а) в правом верхнем углу клеток таблицы поместим цифры простоев ТС, а в левые нижние углы тех же клеток цифры характеризующие количество распределяемых единиц ТС. б) в нижнюю строку исходной отправной таб. Вводится потенциал UВj, а в правый крайний столбец вводится потенциал UАi. * правило заполнения строк: а) при заполнение первой строки выбираем направление то, время простоя минимально, т.е А1и Б4, здесь время простоев имеет стоимость С1 4=3. Количество машин на этом направлении устанавливаются как минимальный из их общего количества имеющая на А1 и потребного для Б4=7ед. При таком распределении достигается либо полный расход ТС, данной базы, либо полное насыщение данного объекта. В данной задачи полностью насыщается объект Б4. На базе А1 остается 4ед. б) остаток ТС на базе А1 целесообразно направить на объект Б3 и по первому плану составляет количество простоев. в) т.к все ресурсы А1 исчерпаны, а в направлении А1 Б3 остаются потребности в 5ед. Используя правила выше изложенные заполним строки в направлении А2 иА3. Проверяем теперь соблюдение условий потенциалов для свободны клеток с этой целью просуммируем для каждой из них соотношения потенциалы баз и объектов и сравним их значения с временем простоев проставленных в таб. 12.1. Проверка соблюдений условий потенциалов для свободных клеток UБ3=С13-UА1=5-0=5 UБ4=С14-UА1=3-0=3 UА3=С33-UБ3=1-5=-4 UБ2=С23-UА3=3-(-4)=7 UА2=С22-UБ2=4-7=-3 UБ1=С21-UА2=2-(-3)=5 Сравним значения суммы потенциалов баз UА1+UБ1 UА1+UБ2 UА3+UБ1 UА2+UБ3 UА2+UБ4 UА3+UБ4 Этот план транспортировки распределения средств по объектам и базам является оптимальным, в случаи если хотя бы в одной из клеток нарушены условия по стоимостям простоя, то план подлежит улучшению путеи перехода к следующей итерациональной процедуре. Резюме: Из изложенного видно, что оптимизация плана распределения ТС в процессе РУР для транспортной задачи по критерию min простоя сводится в 4 этапа: 1 этап Составление описание задачи и отправной таблицы по строкам. 2 этап Расчет потенциалов 3 этап Расчет псевдо стоимости 4 этап Проверка оптимальности переход к улучшению плана в случаи нарушения условий хотя бы в одной клетке.
|
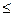(Cij*Хij) (12.2)
UАi и 
