Вероятностные методы принятия решений в задачах оптимизации закупок
Вероятность какого-либо события – это отношение количества исходов (m) в опытах к общему количеству опытов (n). P = m/n 16.1. Априорная вероятность (доопытная) – вероятность события до проведения эксперимента. Апостериорная вероятность (послеопытная) - вероятность наступления события в конце эксперимента. Безусловная вероятность – вероятность наступления события, не связанного в опыте ни с каким другим событием. ( Условная вероятность – вероятность события T при условии, что произошло событие S. ( Формула полной вероятности:
Формула Байеса:
Пример. Прогноз погоды на 12 июня показал, что день будет солнечным (событие P P
Обычно такой класс задач подразумевает наличие трех видов критериев в принятии решений: 1. max-max (т.е. максимальный из максимумов); 2. min-max (минимальный из максимумов); 3. max-min (максимальный из минимумов). Используя такого плана критериев, можно оперировать при решении задач оптимизации закупок, оптимизации создания резерва запасов и других аналогичных задач. Можно использовать как вероятностный подход, так и без учета вероятности. При вероятностном подходе часто используется статистическая средняя математического ожидания, имеющая вид:
Пример. Определить среднюю длину куска ткани, если результаты замеров представлены в таблице:
|

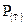 ).
).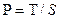 ).
).
 (16.2),
(16.2), 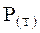 - безусловная вероятность события T;
- безусловная вероятность события T;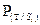 - условная вероятность того, что событие Т наступит при наступлении события
- условная вероятность того, что событие Т наступит при наступлении события 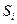 ;
;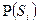 - априорная вероятность события
- априорная вероятность события  (16.3)
(16.3)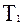 ). Этот прогноз может быть ошибочным с условными вероятностями P(
). Этот прогноз может быть ошибочным с условными вероятностями P(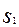 )=0.9 и P(
)=0.9 и P(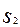 )=0.3; апостериорные вероятности событий:
)=0.3; апостериорные вероятности событий: 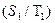 =(0.9*0.8)/(0.9*0.8)+(0.3*0.2)=0.923 – вероятность солнца;
=(0.9*0.8)/(0.9*0.8)+(0.3*0.2)=0.923 – вероятность солнца;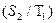 =1-0.923=0.0769 – вероятность, что пойдет дождь.
=1-0.923=0.0769 – вероятность, что пойдет дождь.  (16.4).
(16.4).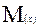 = (42*0,05)+(41*0,15)+(40*0,6)+(39*0,1)+(38*0,08)+(37*0,02)=40,5м
= (42*0,05)+(41*0,15)+(40*0,6)+(39*0,1)+(38*0,08)+(37*0,02)=40,5м


