Нелинейное программирование в задачах распределения разнородных ресурсов.
Нелинейное программирование (НП) – это математические методы определения max или min целевой функции при наличии ограничений в виде неравенств или уравнений. Целевая функция или хотя бы одно из ограничений – нелинейное. Смысл решения задач НП заключается в определении условий, обращающих ЦФ в экстремум. Нелинейное программирование НП – это метод выбора наилучшего плана распределения неоднородных ресурсов, доставляющий в экстремум ЦФ. Методом НП решаются задачи распределения неоднородных ресурсов при следующей формулировке её в общем виде. Пусть имеется m разнородных ресурсов, которое предполагается распределить по n потребителям. Известны либо оценочные, либо вероятностные возможности переработки i-ого ресурса j-ым потребителем, а так же эффективность использования Эij
Распределение ресурсов по потребителям характеризуется параметром управления
требуется распределит ресурсы по потребителям так (т.е. выбрать такие значения Uij), что бы величина:
Рассмотрим первый случай. Для него
Где xij –кол-во ресурсов i-ого типа, назначенные j-ому потребителю при ограничения
Где Ni – кол-во единиц ресурса i-ого вида
Задача Даны 2 группы разнородных ресурсов (m=2), которые можно включить в 3 проекта (n=3)
В первой группе ресурсов 6 единиц (N1=6); во второй группе – 10 ед. (N2=10).
Оценки важности проектов заданы таблицей.
Эффективность вложений ресурсов различного рода Эij задана в таблице
Распределение ресурсов по проектам характеризуется исходной матрицей А = ||Xij|| Требуется распределить разнородные ресурсы так по проектам, чтобы ЭΣ=max
Решение выполняется итерационным процессом Алгоритм решения:
это и будет решение близкое с заданной точностью приближения Е.
реализация расчётов по алгоритму.
где, А0 – матрица, характеризующая отправное распределение ресурсов по проектам.
Примечание: в качестве отправного распределения может быть взято любое (и произвольное в том числе) распределение с ограничительным условием задачи.
Чем отправное распределение ближе к оптимальному, тем меньше итераций понадобится. Берём произвольно Столбцы – номера проектов Строки – номера видов ресурсов
Далее осуществляется итерационная процедура. В результате выполнения к – итераций, получается К-ое приближение к оптимальному.
S(K)=||Sij(K)||, где Sij(K)= Величина Резюме: при заданном Е критерии 0,01 необходимо после шага 4 итерации. В которых Δ(K) больше Е кроме 4-ой итерации.
Точность приближения к оптимуму определяются ЛПР и Е может ровняться и 0,02; и 0,01; и 0,1; и 0,2. Примечание: в курсовых работах точность должна быть не менее 0,1.
|

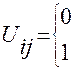 , где 0 – если i-ый ресурс не направляется j-ому потребителю, а 1 –наоборот
, где 0 – если i-ый ресурс не направляется j-ому потребителю, а 1 –наоборот (13.1)
(13.1)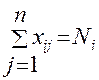 (13.2)
(13.2)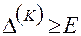 , то путём построения, так называемого, возможного направления и определения в этом направлении конечного шага приближения к оптимуму, получают новое допустимое решение, которое увеличиное значение макс.функции.
, то путём построения, так называемого, возможного направления и определения в этом направлении конечного шага приближения к оптимуму, получают новое допустимое решение, которое увеличиное значение макс.функции.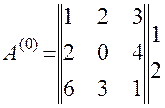
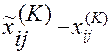
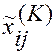 находится с помощью матрицы yij(K).
находится с помощью матрицы yij(K).


