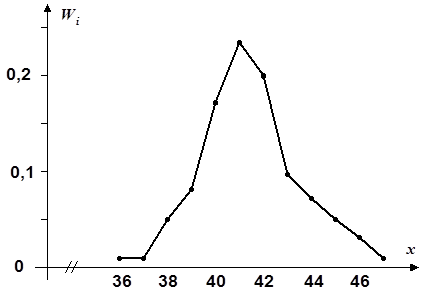Тема 8 Выборочный метод
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. При этом иногда возможно проведение сплошного обследования, то есть обследуют каждый из объектов совокупности относительно изучаемого признака. Однако на практике сплошное обследование применяется сравнительно редко. Оно невозможно по следующим причинам. Во-первых, если обследование объекта связано с его уничтожением (например, проверка на качество консервированной продукции). Во-вторых, если совокупность содержит очень большое число объектов. В-третьих, если сплошное обследование требует больших материальных затрат. По этим причинам из всей совокупности объектов, которую называют генеральной совокупностью, случайно отбирают ограниченное число объектов, которые называют выборочной совокупностью или выборкой, и подвергают их изучению. Объемом генеральной совокупности или выборки называют число входящих в них объектов. При образовании выборки можно поступить двумя способами: 1) после отбора объекта в выборку и его изучения объект возвращается в генеральную совокупность; такую выборку называют повторной; 2) после отбора объекта в выборку и его изучения объект не возвращается в генеральную совокупность; такую выборку называют бесповторной. Организованная выборка должна быть репрезентативной для того, чтобы правильно представлять все пропорции генеральной совокупности. В силу закона больших чисел выборка будет репрезентативной, если ее осуществлять случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Пусть из генеральной совокупности извлечена выборка объема Вариантами называют наблюдаемые значения признака Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. По характеру распределения выделяют дискретны е и непрерывные (или интервальные) вариационные ряды. Эмпирической функцией распределения называют функцию
Для наглядного представления статистического распределения выборки строят полигон частот (для дискретного вариационного ряда) или гистограмму частот (для непрерывного вариационного ряда). Полигоном частот называют ломаную, отрезки которой соединяют точки ( Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы h и с высотами, равными плотности частот Пример 1. Получено распределение размера Таблица1.
Построить полигон относительных частот и найти эмпирическую функцию по данному распределению выборки. Объем выборки найдем как сумму частот Тогда: Таблица 2.
 
Построим полигон относительных частот.
|

 , причем
, причем  наблюдалось
наблюдалось  раз,
раз, 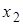 –
–  раз, …,
раз, …,  –
–  раз и
раз и  .
. ; их последовательность, записанная в возрастающем порядке, называется вариационным рядом. Число одинаковых вариант
; их последовательность, записанная в возрастающем порядке, называется вариационным рядом. Число одинаковых вариант  называют частотами (или весами), относительными частотами
называют частотами (или весами), относительными частотами  называют отношение
называют отношение 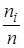 .
. , определяющую для каждого значения
, определяющую для каждого значения  относительную частоту события
относительную частоту события  . Эмпирическая функция распределения служит для оценки теоретической функции распределения генеральной совокупности.
. Эмпирическая функция распределения служит для оценки теоретической функции распределения генеральной совокупности. ).
). .
.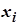

 =100. Относительные частоты найдем как
=100. Относительные частоты найдем как  .
.