Тема 5 Случайные величины
Случайной величиной называют величину, которая в результате испытания примет одно и только одно из своих возможных значений, наперед неизвестное и зависящее от ряда причин. Например: 1) число появлений герба при трех бросаниях монеты: 0, 1, 2, 3; 2) число покупателей магазина: 0, 1, 2, 3, … Дискретной (ДСВ) называют случайную величину, которая принимает отдельные изолированные значения с определенной вероятностью. Законом распределения дискретной случайной величины называется соответствие между ее возможными значениями и их вероятностями:
Часто для описания дискретной случайной величины достаточно знать ее числовые характеристики: математическое ожидание М (Х), дисперсию D (Х) и среднее квадратическое отклонение Математическим ожиданием ДСВ называется сумма произведений всех её возможных значений на соответствующие вероятности:
Математическое ожидание может принимать любые значения и характеризует среднее значение ДСВ. Рассмотрим свойства математического ожидания. Свойство 1. Математическое ожидание постоянной равно самой постоянной Свойство 2. Постоянный множитель можно выносить за знак математического ожидания Свойство 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий Свойство 4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий Замечание. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: Для вычисления удобна формула: Дисперсия характеризует рассеяние значений случайной величины около математического ожидания и может быть только положительной. Средним квадратическим отклонением называется корень квадратный из дисперсии Среднее квадратическое отклонение также характеризует рассеяние значений случайной величины около математического ожидания, но его размерность совпадает с размерностью самой случайной величины Х. . Пример 1. Дискретная случайная величина задана законом распределения.
Найти числовые характеристики Решение. Проверим, что данная таблица является законом распределения:
Найдем числовые характеристики. Математическое ожидание равно:
Дисперсия равна:
Непрерывной случайной величиной (НСВ) называется случайная величина, которая принимает все значения из некоторого конечного или бесконечного промежутка, при этом число ее возможных значений бесконечно. Непрерывная случайная величина задается функцией распределения вероятностей или функцией плотности распределения вероятностей. Функцией распределения вероятностей (интегральной функцией) называется функция F (x), определяющая вероятность того, что случайная величина Рассмотрим некоторые свойства функции распределения. Свойство 1. Значения функции распределения принадлежат отрезку Свойство 2. Функция распределения – неубывающая функция, то есть при Свойство 3. Вероятность того, что НСВ примет значение, заключенное в интервале
Плотностью распределения вероятностей НСВ называется функция f (x), равная первой производной от функции распределения F (x):
Рассмотрим свойства функции плотности. Свойство 1. Плотность распределения вероятностей есть неотрицательная функция Свойство 2. Вероятность того, что НСВ примет значение, заключенное в интервале
Непрерывная случайная величина может быть охарактеризована ее числовыми характеристиками. Математическое ожидание НСВ вычисляется по формуле
Дисперсия НСВ вычисляется по формуле
Среднее квадратическое отклонение НСВ есть корень квадратный из дисперсии
Пример 2. Непрерывная случайная величина задана функцией распределения вероятностей
Найти числовые характеристики и вероятность того, что НСВ попадет в интервал Найдем функцию плотности распределения вероятностей
Тогда математическое ожидание равно:
Найдем дисперсию:
Среднее квадратическое отклонение равно:
Вероятность того, что НСВ попадет в интервал (1; 1,5) найдем следующим образом:
|

 .
. .
.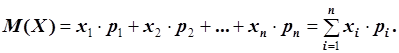
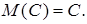
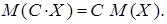


 .
.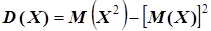 – математическое ожидание квадрата случайной величины минус квадрат математического ожидания или
– математическое ожидание квадрата случайной величины минус квадрат математического ожидания или  .
. .
. .
.
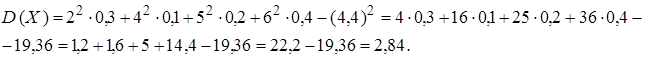 Cреднее квадратическое отклонение равно:
Cреднее квадратическое отклонение равно:  .
.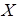 в результате испытаний примет значения, меньшие некоторого значения х, то есть
в результате испытаний примет значения, меньшие некоторого значения х, то есть  .
. , то есть
, то есть 

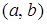 , равна приращению функции распределения на этом интервале, то есть
, равна приращению функции распределения на этом интервале, то есть  .
.
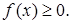
 .
.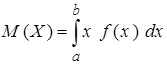 .
. .
.
 .
.



 .
.



