Тема 9 Статистические оценки параметров распределения
Пусть требуется изучить количественный признак генеральной совокупности. Из теоретических соображений и по виду гистограммы или полигона частот установлено, что изучаемый признак распределен в генеральной совокупности по нормальному закону. Тогда необходимо оценить математическое ожидание и среднее квадратическое отклонение, то есть параметры, определяющие нормальное распределение. Для того чтобы статистическая оценка, найденная по данным выборки, давала «хорошее» приближение оцениваемого параметра, она должна удовлетворять следующим трем требованиям: быть несмещенной, эффективной и состоятельной. Несмещенной называют статистическую оценку Эффективной называют статистическую оценку, которая при заданном объеме выборки имеет наименьшую возможную дисперсию. Состоятельной называют статистическую оценку, которая при Для изучения генеральной совокупности относительно количественного признака Точечная оценка представляет из себя приближённое значение оцениваемого параметра и определяется одним числом. Выборочной средней
Выборочная средняя Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения
и среднее квадратическое отклонение Выборочную дисперсию Для малых выборок
и исправленное стандартное отклонение:
Вычисление выборочных характеристик Для сравнения различных вариационных рядов служит коэффициент вариации
Вычислим точечные характеристики для примеров 1 и 2 темы 8. Пример 1 (продолжение). Составим расчетную таблицу 1. Таблица 1
Вычислим:
По расчетам видно, что для выборки объема в 100 единиц выборочный стандарт и исправленный стандарт отличаются незначительно.
Пример 2. Получено распределение людей по росту: Таблица 1
Построить гистограмму частот по данному распределению. Определить точечные оценки параметров распределения. Решение:Найдем плотности частот h = 152–146=6: Таблица 2
Гистограмма частот. ni/h
От интервального ряда перейдем к ряду дискретному, найдя для каждого частичного интервала середину: х 1=(146+152):2=149 и т. д. Составим расчетную таблицу 2.
Вычислим среднее выборочное
выборочную дисперсию
и выборочный стандарт
Коэффициент вариации
|

 , математическое ожидание которой равно оцениваемому параметру
, математическое ожидание которой равно оцениваемому параметру  при любом объеме выборки:
при любом объеме выборки:  .
. стремится по вероятности к оцениваемому параметру.
стремится по вероятности к оцениваемому параметру. извлечена выборка объема
извлечена выборка объема  .
. называют среднее арифметическое взвешенное значение признака выборочной совокупности и вычисляется по формуле:
называют среднее арифметическое взвешенное значение признака выборочной совокупности и вычисляется по формуле: .
. есть несмещенная, эффективная и состоятельная оценка генеральной средней
есть несмещенная, эффективная и состоятельная оценка генеральной средней  .
. , вводят выборочную дисперсию, которую вычисляют по формуле
, вводят выборочную дисперсию, которую вычисляют по формуле
 , которое в математической статистике часто называют выборочным стандартом.
, которое в математической статистике часто называют выборочным стандартом. и отклонение
и отклонение  вычисляют для больших выборок
вычисляют для больших выборок  .
. вычисляют исправленную дисперсию
вычисляют исправленную дисперсию  :
:


 и
и  часто называют первичной статистической обработкой результатов наблюдений.
часто называют первичной статистической обработкой результатов наблюдений. или
или  : тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше.
: тот из рядов имеет большее рассеяние по отношению к выборочной средней, у которого коэффициент вариации больше.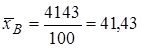 ,
,  ,
, ,
,  ,
, 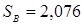 ,
,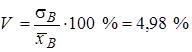 .
.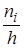 , где ширина частичных интервалов
, где ширина частичных интервалов



 см – средний рост людей данной группы;
см – средний рост людей данной группы;
 cм характеризует абсолютный разброс выборочных данных вокруг среднего.
cм характеризует абсолютный разброс выборочных данных вокруг среднего.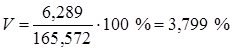 характеризует относительный разброс выборочных данных вокруг среднего.
характеризует относительный разброс выборочных данных вокруг среднего.


