Тема 3 Полная вероятность. Формула Байеса
Если событие А может наступить при появлении одного из несовместных событий
Пусть произведено испытание, в результате которого появилось событие А. Неизвестно, какое из несовместных событий
Пример 1. Три линии упаковывают молоко. Их производительности относятся как 1: 2: 3. Брак на первой линии составляет 0,5% от объёма продукции; на второй – 0,3%; на третьей – 0,25%. Продукция поступает на общий склад. Какова вероятность того, что наудачу взятый пакет оказался с браком? Взятый пакет оказался с браком. Что вероятнее, он упакован на первой, второй или на третьей линии? Введем события: А – {наудачу взятый пакет оказался с браком}, В 1–{пакет упакован на первой линии}, В 2–{пакет упакован на второй линии}, В 3–{пакет упакован на третьей линии}, Тогда
Вероятность события А найдем по формуле полной вероятности для трех событий
Вероятности того, что бракованный пакет упакован на 1-ой, 2-ой или 3-ей линиях найдем по формуле Байеса
И так, вероятность того, что наудачу взятый пакет с браком
Сравнивая вероятности
|

 образующих полную группу, причем вероятности этих событий
образующих полную группу, причем вероятности этих событий  известны и известны условные вероятности
известны и известны условные вероятности  то по формуле полной вероятности можно найти вероятность события А:
то по формуле полной вероятности можно найти вероятность события А:
 полной группы предшествовало ему, назовем их гипотезами. Тогда их вероятности вычисляются по формуле Бейеса
полной группы предшествовало ему, назовем их гипотезами. Тогда их вероятности вычисляются по формуле Бейеса



 ,
,  ,
,  .
. :
:
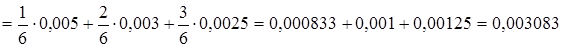 .
. ;
;


 и
и  , делаем вывод: вероятнее, что бракованный пакет упакован на 3-ей линии.
, делаем вывод: вероятнее, что бракованный пакет упакован на 3-ей линии.


