Тема 6 Закон нормального распределения.
Нормальный закон распределения занимает среди других законов распределения особое положение и является наиболее часто встречающимся на практике. Главная его особенность состоит в том, что он является предельным Нормальным называется распределение вероятностей непрерывной величины Х, которое описывается плотностью распределения вида
где График функции плотности нормального распределения называется кривой Гаусса и зависит от параметров
При решении практических задач часто возникает необходимость определения вероятности
где Ф(z)– функция Лапласа. Используя эту формулу, найдем вероятность отклонения случайной величины
Пример. Производителю электроламп известно, что средний срок работы лампы составляет 600 часов, а среднее квадратическое отклонение срока работы – 40 часов. Какова вероятность, что срок работы лампы составит: 1) от 550 до 700 часов; 2) менее 550 часов; 3) отклонится от среднего на величину, меньшую 10 часов? Запишем данные задачи: 1)
Таким образом, около 89% ламп проработают от 550 до 700 часов.
2) Менее 550 часов, следовательно
Таким образом, около 11% ламп проработают менее 550 часов. 3)
То есть около 20% ламп проработают от 590 до 610 часов.
|

 законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях.
законом, к которому приближаются другие законы распределения при часто встречающихся типичных условиях.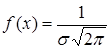
 ,
,  – математическое ожидание,
– математическое ожидание, 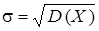 – среднее квадратическое отклонение НСВ
– среднее квадратическое отклонение НСВ 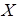 и являются параметрами нормального распределения.
и являются параметрами нормального распределения. и
и  . Легко показать, что функция
. Легко показать, что функция 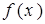 имеет максимум в точке
имеет максимум в точке  и
и 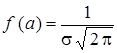 . Поскольку функция
. Поскольку функция  , то ее график будет симметричен относительно прямой
, то ее график будет симметричен относительно прямой  функция
функция  и ее график приближается к оси абсцисс. График плотности нормального распределения, называемый нормальной кривой или кривой Гаусса, приведён на рис. 1.
и ее график приближается к оси абсцисс. График плотности нормального распределения, называемый нормальной кривой или кривой Гаусса, приведён на рис. 1.
 попадания нормально распределенной случайной величины
попадания нормально распределенной случайной величины  , которая вычисляется по формуле:
, которая вычисляется по формуле: ,
,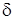 :
:
 .
.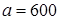 часов,
часов,  часов.
часов. ,
, 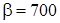 часов. Тогда
часов. Тогда
 .
. ,
,  . Тогда
. Тогда
 .
.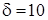 часов,
часов,  .
.


