Тема 11 Элементы теории корреляции
При рассмотрении многих задач требуется оценить зависимость некоторой случайной величины от другой случайной величины. Например, нас интересует соотношение между ростом и весом у определённой группы людей, между ценой и количеством проданного товара. В этих и многих других случаях будет наблюдаться линейная зависимость. Линейные зависимости–простейшие для анализа, поэтому стараются описать связь между случайными величинами посредством линейной модели. Этот процесс несёт название линейной регрессии. Термин “регрессия” используется для описания природы связи. Линейная зависимость может быть функциональной или статистической. Функциональной называется такая зависимость, когда одному значению величины Х соответствует одно значение величины Y. Такая зависимость встречается редко, так как обе величины Х и Y подвержены действию других случайных факторов. Например, товарооборот Y зависит не только от численности населения Х, но и от цен на товары, уровня обслуживания, наличия денег у покупателей и т.д. Статистической называют зависимость, при которой изменение одной из величин влечёт изменение распределения другой величины. Частным случаем статистической зависимости является корреляционная зависимость, которая проявляется в том, что при изменении одной из величин изменяются условные средние значения другой. Термин “корреляция” используется для измерения тесноты связи. При большом числе наблюдений корреляционная зависимость задаётся корреляционной таблицей (см. таблицу 1). Для описания двух случайных величин Х и Y используют их числовые характеристики M (Х) и Корреляционным моментом называется математическое ожидание произведения отклонений этих случайных величин и обозначается
Рассмотрим свойства корреляционного момента. Свойство 1. Корреляционный момент равен математическому ожиданию произведения двух случайных величин без произведения математических ожиданий этих случайных величин:
Свойство 2. Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин Х и Y. Эта особенность корреляционного момента являяется недостатком этой числовой характеристики, поскольку затрудняет сравнение различных систем случайных величин. Для удобства такого сравнения вводят безразмерный коэффициент корреляции. Коэффициентом корреляции двух случайных величин Х и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин и обозначают: К свойствам коэффициента корреляции следует отнести: Свойство 1. Коэффициент корреляции независимых случайных величин Х и Y равен нулю. Свойство 2. Абсолютная величина коэффициента корреляции не превышает 1, то есть По свойству 2 следует, что все значения коэффициента корреляции располагаются между –1 и 1, то есть 1. Если коэффициент корреляции 2. Если 3. Если 4. Если Чем ближе абсолютное значение коэффициента корреляции к единице, тем сильнее зависимость между X и Y.
На практике при изучении зависимости между двумя случайными величинами используют поле корреляции, которое представляет собой диаграмму, на которой изображается совокупность значений двух признаков, соответствующих величинам X и Y. Каждая точка этой диаграммы имеет координаты  , которые соответствуют размерам признака. Построим поле корреляции для , которые соответствуют размерам признака. Построим поле корреляции для  и и  : :
По виду поля корреляции можно предположить, что между признаками X и Y существует линейная зависимость. По данным выборки выборочный коэффициент корреляции
По полученному значению Уравнение линейной зависимости между Х и Y называется выборочнымуравнением прямой линии регрессии и имеет вид:
Угловой коэффициент этой прямой называется выборочным коэффициентом регрессии Y на Х и обозначается:
Параметры уравнения линейной регрессии вычисляются по выборке. Уравнение используется при статистических исследованиях для вычисления предполагаемых средних значениях одного из признаков, когда известно значение другого. Пример 5. Собраны данные о товарообороте Х (ден.ед.) и средних товарных запасах Y (ден.ед.) 12 магазинов.
1. Построить корреляционное поле. 2. Определить выборочный коэффициент корреляции 3. Считая, что между признаками X и Y имеет место линейная зависимость, найти выборочное уравнение регрессии Y на Х и построить полученную прямую на поле корреляции.
Решение: Составим расчетную таблицу для нахождения Найдем суммы по всем столбцам.
Используя полученные результаты, найдем:
Коэффициент корреляции вычислим по формуле
По полученному значению Найдем выборочное уравнение регрессии Y на X:
Построим прямую линию регрессии Y на X по двум точкам. Пусть х =35, тогда Пусть х =80, тогда
Уравнение регрессии позволяет оценить ожидаемое среднее значение товарных запасов в зависимости от товарооборота.
Задача 1 1. В первом ящике находятся шары с номерами 1,2,3,4, во втором – с номерами 5,6,7,8. Из каждого ящика наудачу вынули по одному шару. Какова вероятность того, что сумма номеров равна 11. 2. В коробке содержится 3 одинаковых занумерованных кубика. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлечённых кубиков появятся в возрастающем порядке. 3. Сто лотерейных билетов с номерами от 1 до 100 упакованы в пачку. Найти вероятность того, что порядковый номер наудачу взятого билета, не содержит цифру 0? 4. Бросили два игральных кубика. Какова вероятность, что сумма выпавших очков делится на 4? 5. Бросают две монеты. Какова вероятность, что выпадет два «орла»? 6. В колоде 36 карт. Наудачу вынимают одну. Какова вероятность, что карта окажется тузом? 7. В лотерее на каждые 100 билетов разыгрывается по5 вещевых и 3 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного билета? 8. Играя с кубиками, ребенок составляет их в ряд. Какова вероятность, что из трех кубиков с буквами К,К,О, окажется составлено слово КОК. 9. В каждой из двух урн находится по 8 шаров, пронумерованных от 1 до 8. Из каждой урны вынимают по одному шару. Какова вероятность того, что окажутся вынутыми шары с одинаковыми номерами? 10. Куб, все грани которого окрашены, разрезан на тысячу одинаковых кубиков. Какова вероятность того, что наудачу взятый кубик имеет две окрашенные грани?
|

 (X), M (Y) и
(X), M (Y) и  и коэффициент корреляции
и коэффициент корреляции 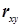 .
. .
. .
. .
. .
. .
. .
. , это свидетельствует о наличии функциональной линейной зависимости между случайными величинами X и Y.
, это свидетельствует о наличии функциональной линейной зависимости между случайными величинами X и Y. и
и  независимы, то
независимы, то  .
. , то между величинами X и Y наблюдается обратная зависимость.
, то между величинами X и Y наблюдается обратная зависимость.
 вычисляется по формуле:
вычисляется по формуле: ,
, .
. .
. ,
,  ,
,  ,
,  и
и  .
.



 у.е. – средний товарооборот данной группы магазинов.
у.е. – средний товарооборот данной группы магазинов. у.е. – средние товарные запасы.
у.е. – средние товарные запасы. среднее квадратическое отклонение.
среднее квадратическое отклонение. среднее квадратическое отклонение.
среднее квадратическое отклонение.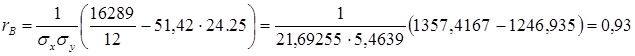
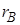 можно сделать вывод о тесноте связи между X и Y: cвязь между товарооборотом и средними товарными запасами сильная, положительная.
можно сделать вывод о тесноте связи между X и Y: cвязь между товарооборотом и средними товарными запасами сильная, положительная. ,
,
 .
. .
. .
.



