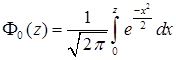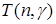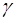Задача 8. Известно распределение студентов группы института по числу пропусков занятий Х час за год (см
Известно распределение студентов группы института по числу пропусков занятий Х час за год (см. табл.). Полагая, что изменчивость величины признака Х описывается законом нормального распределения, требуется:
1. Вычислить выборочное среднее 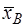 , «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака Х; , «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака Х;
2. Найти доверительный интервал для среднего числа пропусков а на уровне заданной надёжности 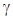 . Сделать анализ полученных результатов. . Сделать анализ полученных результатов.
1. 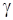 =0,95 =0,95
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
2. 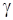 =0,99 =0,99
| Число пропусков
|
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
|
3. 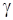 =0,999 =0,999
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
4. 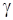 =0,90 =0,90
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
5. 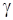 =0,99 =0,99
| Число пропусков
|
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
|
6. 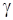 =0,95 =0,95
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
7. 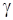 =0,90 =0,90
| Число пропусков
|
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
|
8. 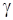 =0,99 =0,99
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
9. 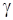 =0,95 =0,95
| Число пропусков
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
10. 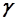 =0,95 =0,95
| Число пропусков
|
|
|
|
|
|
|
| | Число студентов
|
|
|
|
|
|
|
|
Задача 9
Получено распределение работников торгового предприятия по заработной плате Х усл.ед. (см. табл.). Требуется:
1. Построить гистограмму относительных частот для наблюдаемых значений признака Х.
2. Вычислить выборочное среднее 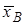 , выборочное стандартное отклонение , выборочное стандартное отклонение 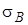 и коэффициент вариации V изучаемого признака. и коэффициент вариации V изучаемого признака.
3. Полагая, что изменчивость величины признака Х описывается законом нормального распределения, найти доверительный интервал для ожидаемого среднего значения а заработной платы работников данного предприятия на уровне надёжности 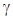 . .
1. 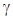 =0,9108 =0,9108
| Зар.плата,
усл.ед.
| 12-14
| 14-16
| 16-18
| 18-20
| 20-22
| 22-24
| 24-26
| 26-28
| | Число людей
|
|
|
|
|
|
|
|
|
2. 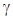 =0,9642 =0,9642
| Зар.плата, усл.ед.
| 10-20
| 20-30
| 30-40
| 40-50
| 50-60
| 60-70
| 70-80
| 80-90
| | Число людей
|
|
|
|
|
|
|
|
|
3. 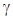 =0,8904 =0,8904
| Зар.плата,
усл.ед.
| 51.5-58.5
| 58.5-65.5
| 65.5-72.5
| 72.5-79.5
| 79.5-86.5
| 86.5-93.5
| 93.5-100.5
| 100.5-107.5
| | Число людей
|
|
|
|
|
|
|
|
|
4. 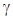 =0,9544 =0,9544
| Зар. плата, усл.ед.
| 25-26
| 26-27
| 27-28
| 28-29
| 29-30
| 30-31
| 31-32
| | Число людей
|
|
|
|
|
|
|
|
5. 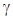 =0,9722 =0,9722
| Зар. плата,
усл. ед.
| 11-19
| 19-27
| 27-35
| 35-43
| 43-51
| 51-59
| 59-67
| 67-75
| | Число людей
|
|
|
|
|
|
|
|
|
6. 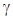 =0,9282 =0,9282
| Зар. плата,
усл. ед.
| 21-29
| 29-37
| 37-45
| 45-53
| 53-61
| 61-69
| 69-77
| 77-85
| | Число людей
|
|
|
|
|
|
|
|
|
7. 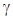 =0,9010 =0,9010
| Зар. плата, усл. ед.
| 51-58
| 58-65
| 65-72
| 72-79
| 79-86
| 86-93
| 93-90
| | Число людей
|
|
|
|
|
|
|
|
8. 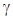 =0,9030 =0,9030
| Зар. плата, усл. ед.
| 55-61
| 61-67
| 67-73
| 73-79
| 79-85
| 85-91
| 91-97
| | Число людей
|
|
|
|
|
|
|
|
9. 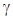 =0,9050 =0,9050
| Зар. плата, усл. ед.
| 25-32
| 32-39
| 39-46
| 46-53
| 53-60
| 60-67
| 67-74
| 74-81
| | Число людей
|
|
|
|
|
|
|
|
|
10. 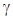 =0,9128 =0,9128
| Зар. плата, усл. ед.
| 45-55
| 55-65
| 65-75
| 75-85
| 85-95
| 95-105
| 105-115
| | Число людей
|
|
|
|
|
|
|
|
Задача 10
Собраны данные о средних товарных запасах Х и товарообороте Y (в условных единицах) однотипных магазинов.
По заданным значениям пар (хi,yi) построить корреляционное поле.
Считая, что между признаками X и Y имеет место линейная зависимость, вычислить коэффициент корреляции 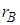 . Сделать вывод о тесноте и направлении связи между X и Y. . Сделать вывод о тесноте и направлении связи между X и Y.
Найти выборочное уравнение регрессии Y на Х и построить полученную прямую на поле корреляции.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Приложение Б. –Таблица значений функции Лапласа 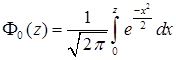
| z
|
|
|
|
|
|
|
|
| ^
|
| | 0,0
| 0,00000
| 0,00399
| 0,00798
| 0,01197
| 0,01595
| 0,01994
| 0,02392
| 0,02790
| 0,03188
| 0,03586
| | 0,1
| 0,03983
| 0,04380
| 0,04776
| 0,05172
| 0,05567
| 0,05962
| 0,06356
| 0,06749
| 0,07142
| 0,07535
| | 0,2
| 0,07926
| 0,08317
| 0,08706
| 0,09095
| 0,09483
| 0,09871
| 0,10257
| 0,10642
| 0,11026
| 0,11409
| | 0,3
| 0,11791
| 0,12172
| 0,12552
| 0,12930
| 0,13307
| 0,13683
| 0,14058
| 0,14431
| 0,14803
| 0^15173
| | 0,4
| 0,15542
| 0,15910
| 0,16276
| 0,16640
| 0,17003
| 0,17364
| 0,17724
| 0,18082
| 0,18439
| 0,18793
| | 0,5
| 0,19146
| 0,19497
| 0,19847
| 0,20194
| 0,20540
| 0,20884
| 0,21226
| 0,21566
| 0,21904
| 0,22240
| | 0,6
| 0,22575
| 0,22907
| 0,23237
| 0,23565
| 0,23891
| 0,24215
| 0,24537
| 0,24857
| 0,25175
| 0,25490
| | 0,7
| 0,25804
| 0,26115
| 0,26424
| 0,26730
| 0,27035
| 0,27337
| 0,27637
| 0,27935
| 0,28230
| 0,28524
| | 0,8
| 0,28814
| 0,29103
| 0,29389
| 0,29673
| 0,29955
| 0,30234
| 0,30511
| 0,30785
| 0,31057
| 0,31327
| | 0,9
| 0,31594
| 0,31859
| 0,32121
| 0,32381
| 0,32639
| 0,32894
| 0,33147
| 0,33398
| 0,33646
| 0,33891
| | 1,0
| 0,34134
| 0,34375
| 0,34614
| 0,34849
| 0,35083
| 0,35314
| 0,35543
| 0,35769
| 0,35993
| 0,36214
| | 1.1
| 0,36433
| 0,36650
| 0,36864
| 0,37076
| 0,37286
| 0,37493
| 0,37698
| 0,37900
| 0,38100
| 0,38298
| | 1,2
| 0,38493
| 0,38686
| 0,38877
| 0,39065
| 0,39251
| 0,39435
| 0,39617
| 0,39796
| 0,39973
| 0,40147
|
Продолжение приложения 2
| z
|
|
|
|
|
|
|
|
| 8,
|
| | 1,3
| 0,40320
| 0,40490
| 0,40658
| 0,40824
| 0,40988
| 0,41149
| 0,41308
| 0,41466
| 0,41621
| 0,41774
| | 1,4
| 0,41924
| 0,42073
| 0,42220
| 0,42364
| 0,42507
| 0,42647
| 0,42785
| 0,42922
| 0,43056
| 0,43189
| | 1,5
| 0,43319
| 0,43448
| 0,43574
| 0,43699
| 0,43822
| 0,43943
| 0,44062
| 0,44179
| 0,44295
| 0,44408
| | 1,6
| 0,44520
| 0,44630
| 0,44738
| 0,44845
| 0,44950
| 0,45083
| 0,45154
| 0,45254
| 0,45352
| 0,45449
| | 1,7
| 0,45543
| 0,45637
| 0,45728
| 0,45818
| 0,45907
| 0,45994
| 0,46080
| 0,46164
| 0,46246
| 0,46327
| | 1,8
| 0,46407
| 0,46485
| 0,46562
| 0,46638
| 0,46712
| 0,46784
| 0,46856
| 0,46926
| 0,46995
| 0,47062
| | 1,9
| 0,47128
| 0,47193
| 0,47257
| 0,47320
| 0,47381
| 0,47441
| 0,47500
| 0,47558
| 0,47615
| 0,47670
| | 2,0
| 0,47725
| 0,47778
| 0,47831
| 0,47882
| 0,47932
| 0,47982
| 0,48030
| 0,48077
| 0,48124
| 0,48169
| | 2,1
| 0,48214
| 0,48257
| 0,48300
| 0,48341
| 0,48382
| 0,48422
| 0,48461
| 0,48500
| 0,48537
| 0,48574
| | 2,2
| 0,48610
| 0,48645
| 0,48679
| 0,48713
| 0,48745
| 0,48778
| 0,48809
| 0,48840
| 0,48870
| 0,48899
| | 2,3
| 0,48928
| 0,48956
| 0,48983
| 0,49010
| 0,49036
| 0,49061
| 0,49086
| 0,49111
| 0,49134
| 0,49158
| | 2.4
| 0,49180
| 0,49202
| 0,49224
| 0,49245
| 0,49266
| 0,49286
| 0,49305
| 0,49324
| 0,49343
| 0,49361
| | 2,5
| 0,49379
| 0,49396
| 0,49413
| 0,49430
| 0,49446
| 0,49461
| 0,49477
| 0,49492
| 0,49506
| 0,49520
| | 2,6
| 0,49534
| 0,49547
| 0,49560
| 0,49573
| 0,49585
| 0,49598
| 0,49609
| 0,49621
| 0,49632
| 0,49643
| | 2,7
| 0,49653
| 0,49664
| 0,49674
| 0,49683
| 0,49693
| 0,49702
| 0,49711
| 0,49720
| 0,49728
| 0,49736
|
Окончание приложения 2
| z
|
|
|
|
|
|
|
|
|
|
| | 2,8
| 0.49744
| 0,49752
| 0,49760
| 0,49767
| 0,49774
| 0,49781
| 0,49788
| 0,49795
| 0,49801
| 0,49807
| | 2,9
| 0,49813
| 0,49819
| 0,49825
| 0,49831
| 0,49836
| 0,49841
| 0,49846
| 0,49851
| 0,49856
| 0,49861
| | 3,0
| 0,49865
| 0,49869
| 0.49874
| 0,49878
| 0,49882
| 0.49886
| 0,49889
| 0,49893
| 0,49896
| 0,49900
| | 3,1
| 0.49903
| 0,49906
| 0.49910
| 0,49913
| 0,49916
| 0,49918
| 0,49921
| 0,49924
| 0,49926
| 0,49929
| | 3,2
| 0.49931
| 0.49934
| 0.49936
| 0,49938
| 0,49940
| 0,49942
| 0,49944
| 0,49946
| 0,49948
| 0,49950
| | 3,3
| 0,49958
| 0,49958
| 0.49955
| 0,49957
| 0,49958
| 0,49960
| 0,49961
| 0,49962
| 0,49964
| 0,49965
| | 3,4
| 0,49966
| 0.49968
| 0.49969
| 0.49970
| 0,49971
| 0,49972
| 0,49973
| 0,49974
| 0,49975
| 0,49976
| | 3,5
| 0,49977
| 0,49978
| 0.49978
| 0.49979
| 0,49980
| 0.49981
| 0,49981
| 0,49982
| 0,49983
| 0,49983
| | 3,6
| 0,49984
| 0,49985
| 0,49985
| 0.49986
| 0,49986
| 0,49987
| 0,49987
| 0,49988
| 0,49988
| 0,49989
| | 3,7
| 0,49989
| 0,49990
| 0,49990
| 0,49990
| 0,49991
| 0,49991
| 0,49992
| 0,49992
| 0,49992
| 0,49992
| | 3,8
| 0,49998
| 0,49993
| 0,49993
| 0,49994
| 0,49994
| 0.49994
| 0.49994
| 0,49995
| 0,49995
| 0,49995
| | 3.9
| 0,49995
| 0,49995
| 0,49996
| 0,49996
| 0.49996
| 0.49996
| 0,49996
| 0,49996
| 0,49997
| 0,49997
| | 4,0
| 0,499968
| | 4.5
| 0.49997
| | 5,0
| 0,4999997
|
Приложение Г Таблица значений коэффициента 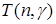

| 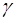
| | 0,90
| 0,95
| 0,98
| 0,99
| |
| 1,83
| 2,26
| 1,15
| 3,25
| |
| 1,81
|
|
|
| |
| 0,47
| 0,65
| 0,92
| 1,08
|
ЛИТЕРАТУРА
Основная литература
| 1. Гмурман, В. Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман. - 12-е изд., перераб. - М.: Юрайт, 2010. - 479 с.
2. Гмурман, В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для вузов / В. Е. Гмурман. - 11-е изд., перераб. - М.: Юрайт, 2010. - 404 с.
3. Красс М. С. Математика для экономического бакалавриата: учебник / М. С. Красс, Б. П. Чупрунов. – М.: Дело, 2005. – 576 с.
| Дополнительная литература
| 1. Подопригора, В. Г. Теория вероятностей. Случайные функции. Марковские процессы: учеб. пособие для студентов по специальностям 080507.65, 080105.65, 080109.65, 080301.65 и направлениям подготовки 080100.62, 080500.62 всех форм обучения / В. Г. Подопригора, Е. А. Попова, С. А. Раковская. - Красноярск: КГТЭИ, 2009. - 80 с.
2. Попова, Е. А. Элементы комбинаторики: практикум / Е. А. Попова, С. А. Раковская; Краснояр. гос. торг.-экон. ин-т. - Красноярск: КГТЭИ, 2008. - 43 с.
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|
Шов первичный, первично отсроченный, вторичный (показания) В зависимости от времени и условий наложения выделяют швы:
1) первичные...
Предпосылки, условия и движущие силы психического развития Предпосылки –это факторы. Факторы психического развития –это ведущие детерминанты развития чел. К ним относят: среду...
Анализ микросреды предприятия Анализ микросреды направлен на анализ состояния тех составляющих внешней среды, с которыми предприятие находится в непосредственном взаимодействии...
|
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...
Тактические действия нарядов полиции по предупреждению и пресечению групповых нарушений общественного порядка и массовых беспорядков В целях предупреждения разрастания групповых нарушений общественного порядка (далееГНОП) в массовые беспорядки подразделения (наряды) полиции осуществляют следующие мероприятия...
|
|

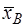 , «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака Х;
, «исправленное» стандартное отклонение S (X) и коэффициент вариации V изучаемого признака Х;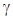 . Сделать анализ полученных результатов.
. Сделать анализ полученных результатов.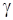 =0,95
=0,95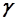 =0,95
=0,95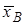 , выборочное стандартное отклонение
, выборочное стандартное отклонение 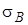 и коэффициент вариации V изучаемого признака.
и коэффициент вариации V изучаемого признака.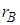 . Сделать вывод о тесноте и направлении связи между X и Y.
. Сделать вывод о тесноте и направлении связи между X и Y.