Министерство образования Республики Беларусь 7 страница
4.3. Решение типового варианта контрольной работы N 3
Задача 3.1. Найти градиент и уравнения касательной плоскости и нормали к заданной поверхности
Решение. Обозначим Тогда
Величина градиента
Уравнение касательной плоскости, имеющей нормальный вектор (7,-4,-19) и проходящей через
или
Нормальная прямая имеет направляющий вектор (7,-4,-19) и проходит через
Задача 3.2. Найти наибольшее и наименьшее значения функции
Решение. Область D показана на рисунке (треугольник OAB).
y
B(0,6)
D
0 2 A(3,0) x
Cтационарные точки являются решениями системы уравнений
откуда находим точку Исследуем функцию на границе области D. Отрезок ОА. Здесь
На концах отрезка
Отрезок АВ. Здесь
При
Отрезок ОВ. Здесь Из результатов (2)-(6) заключаем, что
причем наибольшее значение достигается в точке А(3,0), наименьшее - в точке С(2,1).
Задача 3.3. Найти полный дифференциал функции
Решение. Частные производные равны
Поэтому
Задача 3.4. Найти частные производные второго порядка функции Решение. Сначала находим частные производные первого порядка:
Затем, дифференцируя найденные частные производные, получим частные производные второго порядка данной функции:
Задача 3.5. Вычислить значение производной сложной функции
где
при
Решение. Так как сложная функция
Вычислим
Подставим значения
4.4. Решение типового варианта контрольной работы № 4
Задача 4.1. С помощью интегрирования по частям вычислить неопределенный интеграл от функции вида Решение. Поскольку
искомый интеграл равен
Задача 4.2. Вычислить неопределенный интеграл с помощью разложения на простейшие дроби подынтегральной функции Решение. Поскольку степень многочлена в числителе не меньше степени знаменателя, следует выполнить деление:
Правильную дробь разложим на простейшие дроби
Методом неопределенных коэффициентов находим
откуда
Решая эту систему уравнений, имеем
Искомый интеграл равен
Задача 4.3. Вычислить с помощью подстановки неопределенный интеграл от функции Решение. Выполним подстановку Тогда искомый интеграл запишется: Разлагая подынтегральное выражениe на простейшие дроби
и раскрывая скобки в равенстве
приходим к соотношению
Система уравнений относительно
Решая ее методом Гаусса, находим Искомый интеграл равен:
Задача 4.4. Вычислить с помощью подстановки неопределенный интеграл от функции Решение. Универсальной является подстановка
Поэтому искомый интеграл сводится к случаю интегрирования рациональной дроби
Однако в ряде случаев более удобны подстановки:
(1) (2) (3)
Подстановки 1,2 приводят к подынтегральным выражениям, содержащим радикал, и поэтому нецелесообразны. Для подстановки 3 приходим к интегралу, более простому, чем (7), и легко приводящемуся к табличному:
Задача 4.5. Вычислить площадь фигуры, ограниченной линиями:
а) б)
Решение. а). Рассмотрим вспомогательную функцию
Исследуем
нетрудно проверить, что
Вычисляя интеграл по частям, находим
Поэтому б). Здесь
Вычисляем неопределенный интеграл
Тогда
Задача 4.6. Вычислить площадь, ограниченную кривой
Решение. Кривая определена для тех значений
Области (8) принадлежат интервалу
Площадь вычисляется по формуле
Вычисляя неопределенный интеграл
находим
Задача 4.7. Вычислить несобственный интеграл
Решение. Согласно определению несобственного интеграла с бесконечным пределом имеем
Поскольку корнями трехчлена в знаменателе будут
Методом неопределенных коэффициентов находим
Значение несобственного интеграла равно
Задача 4.8. Вычислить массу неоднородной пластины, ограниченной заданными линиями и имеющей поверхностную плотность
D:
Решение. Вид области показан на рисунке.
0 D 1
Масса пластины
|

 О
О 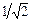
 в точке
в точке  .
.
 .
.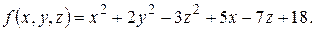






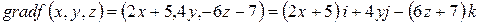 ;
;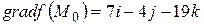 .
.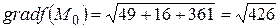 .
. , запишется
, запишется ,
, .
.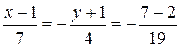 .
. в области D, ограниченной заданными линиями:
в области D, ограниченной заданными линиями:






 1 С
1 С
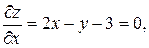
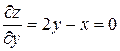 ,
,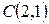 , принадлежащую, как видно из рисунка, области
, принадлежащую, как видно из рисунка, области  . В этой точке
. В этой точке  . (2)
. (2)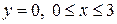 и
и  Стационарные точки определяются из уравнения
Стационарные точки определяются из уравнения 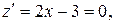 откуда
откуда  В этой точке
В этой точке . (3)
. (3)
 ,
,  . (4)
. (4) и
и 
 Из уравнения
Из уравнения  находим
находим 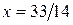 и
и . (5)
. (5) имеем
имеем . (6)
. (6) Поскольку
Поскольку  при
при  функция не имеет стационарных точек. Значения ее при
функция не имеет стационарных точек. Значения ее при 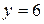 были вычислены в (4), (6).
были вычислены в (4), (6).



 .
.





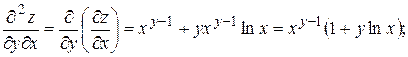

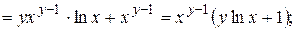
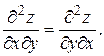


 ,
, с точностью до двух знаков после запятой.
с точностью до двух знаков после запятой. зависит от одной переменной
зависит от одной переменной  через промежуточные переменные
через промежуточные переменные  и
и  , которые в свою очередь зависят от одной переменной
, которые в свою очередь зависят от одной переменной  то вычисляем полную производную этой функции по формуле
то вычисляем полную производную этой функции по формуле .
.
 .
. :
:
 .
. в выражение производной. Получим
в выражение производной. Получим .
.



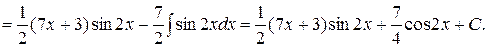

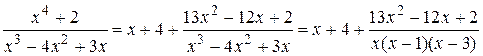 .
. .
. ,
,
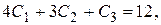
 .
.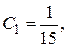

 .
.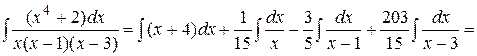

 .
.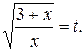 Разрешая уравнение относительно
Разрешая уравнение относительно 
 .
.

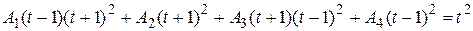 ,
,
 запишется
запишется
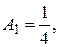


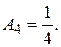


 .
.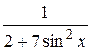 .
.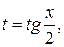 для которой нетрудно проверить равенства
для которой нетрудно проверить равенства
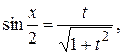



 . (7)
. (7) Тогда
Тогда 
 ;
;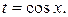 Тогда
Тогда 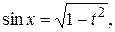
 ;
; Тогда
Тогда 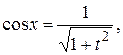

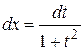 .
. .
.
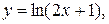





 на отрезке
на отрезке 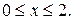 Площадь вычисляется по формуле
Площадь вычисляется по формуле 
 Очевидно, что
Очевидно, что  Поскольку
Поскольку ,
, достигает в точке
достигает в точке  локального минимума, причем
локального минимума, причем 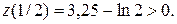 Кроме того,
Кроме того,  Поэтому наименьшее значение
Поэтому наименьшее значение  , положительно, и, значит,
, положительно, и, значит,  Имеем
Имеем

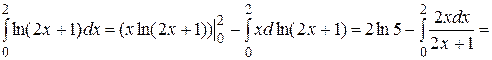
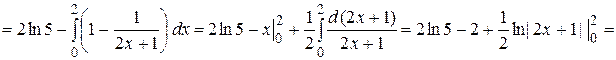


 на
на  Имеем
Имеем 
 , и, следовательно,
, и, следовательно, 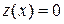 находим значение
находим значение  поэтому
поэтому  при
при  и
и  при
при  Искомая площадь равна:
Искомая площадь равна: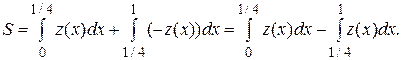

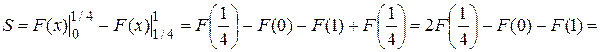
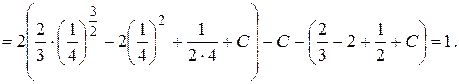
 в полярной системе координат.
в полярной системе координат. из интервала
из интервала  (или
(или  ), при которых выполняется условие
), при которых выполняется условие  Неравенство
Неравенство  имеет решения
имеет решения 
 или
или . (8)
. (8) т.е.
т.е.



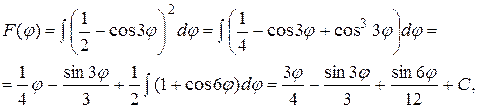
 .
. или доказать его расходимость.
или доказать его расходимость. .
.
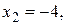 то
то .
.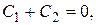
 , откуда
, откуда 
 Поэтому
Поэтому
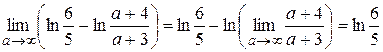 .
.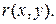


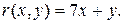
 Y
Y
 8
8


 y=8x2
y=8x2

 X
X запишется с помощью двойного интеграла
запишется с помощью двойного интеграла


