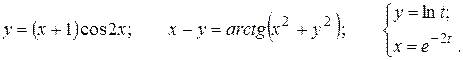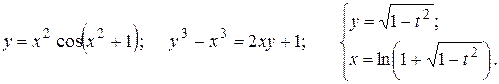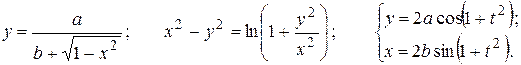Министерство образования Республики Беларусь 2 страница
1. a = 2i - 3j + k, b = j + 4k, с = 5i + 2j - 3k.
2. а = 3i + 4j + k, b = i - 2j + 7k, с = 3i - 6j + 21k.
3. a = 2i - 4j - 2k b = 7i + 3j c = 3i + 5j - 7k.
4. а= -7i + 2k, b = 2i - 6j + 4k, c = i-3j + 2k.
5. а = -4i + 2j - k, b = 3i + 5j - 2k, c = j + 5k.
6. a = 3i - 2j + k, b = 2j - 3k, c = -3i + 2j - k.
7.a = 4i – j + 3k, b = 2i + 3j - 5k, c = 7i + 2j + 4k. 8. a = 4i + 2j - 3k, b = 2i + k, с = -12i - 6j + 9k.
9. a = -i + 5k, b = -3i + 2j + 2k, с = -2i - 4j + k.
10. a = 6i - 4j + 6k, b = 9i - 6j + 9k, с = i - 8k.
11. a = 5i - 3j + 4k, b = 2i - 4j - 2k, c = 3i + 5j - 7k.
12. а = -4i + 3j - 7k, b = 4i + 6j - 2k, с = 6i + 9j - 3k.
13. а= -5i + 2j - 2k, b = 7i - 5k, c = 2i + 3j - 2k.
14. a = -4i - 6j + 2k, b = 2i + 3j - k, c = -i + 5j - 3k.
15. a = -4i + 2j - 3k, b = -3j + 5k, с = 6i + 6j -4k.
16. а = -3i + 8j, b = 2i + 3j - 2k, c = 8i + 12j - 8k.
17. a = 2i - 4j - 2k, b = -9i + 2k, c = 3i + 5j - 7k.
18. a = 9i - 3j + k, b = 3i - 15j + 21k, c = i - 5j + 7k.
19. а = -2i + 4j - 3k, b = 5i + j - 2k, c = 7i + 4j – k.
20. а = -9i + 4j - 5k, b = i - 2j + 4k, c = -5i + 10j - 20k.
21. a = 2i - 7j + 5k, b = -i + 2j - 6k, c = 3i + 2j - 4k.
22. a = 7i - 4j - 5k, b = i - 11j + 3k, с = 5i + 5j + 3k.
23. a = 4i - 6j - 2k, b = -2i + 3j + k, c = 3i - 5j + 7k.
24. a = 3i – j + 2k, b = -i + 5j - 4k, c = 6i - 2j + 4k.
25. а = -3i – j - 5k, b = 2i - 4j + 8k, c = 3i + 7j – k.
26. а = -3i + 2j + 7k, b = i - 5k, c = 6i + 4j – k.
27. a = 3i – j + 5k, b = 2i - 4j + 6k, c = i - 2j + 3k. 28. a = 4i - 5j - 4k, b = 5i - j, c = 2i + 4j - 3k.
29. а = -9i + 4k, b = 2i - 4j + 6k, c = 3i - 6j + 9k.
30. a = 5i - 6j - 4k, b = 4i + 8j - 7k, c = 3j - 4k.
Задание 1.5
Даны четыре точки А 1( а) плоскости А 1 А 2 А 3; б) прямой А 1 А 2; в) прямой А 4 М, перпендикулярной к плоскости А 1 А 2 А 3; г) прямой А 3 N, параллельной прямой А 1 А 2; д) плоскости, проходящей через точку А 4 перпендикулярно к прямой А 1 А 2. Вычислить: е) синус угла между прямой А 1 А 4 и плоскостью А 1 А 2 А 3. ж ) косинус угла между координатной плоскостью Оху и плоскостью А 1 А 2 А 3.
1. А1(3, 1, 4), А2(-1, 6, 1), А3(1, 1, 6), А4(0, 4, -1).
2. А1(3, 5, 4), А2(5, 8, 3), А3(1, 2, -26), А4(-1, 0, 2).
3. А1(2, 4, 3), А2(1, 1, 5), А3(4, 9, 3), А4(3, 6, 7).
4. А1(9, 5, 5), А2(-3, 7, 1), А3(5, 7, 8), А4(6, 9, 2).
5. А1(0, 7, 1), А2(2, -1, 5), А3(1, 6, 3), А4(3, -9, 8).
6. А1(5, 5, 4), А2(1, -1, 4), А3(3, 5, 1), А4(5, 8, -1).
7. А1(6, 1, 1), А2(4, 6, 6), А3(4, 2, 0), А4(1, 2, 6).
8. А1(7, 5, 3), А2(9, 4, 4), А3(4, 5, 7), А4(7, 9, 6).
9. А1(6, 8, 2), А2(5, 4, 7), А3(2, 4, 7), А4(7, 3, 7).
10. А1(4, 2, 5), А2(0, 7, 1), А3(0, 2, 7), А4(1, 5, 0).
11. А1(4, 4, 10), А2(7, 10, 2), А3(2, 8, 4), А4(9, 6, 9).
12. А1(4, 6, 5), А2(6, 9, 4), А3(2, 10, 10), А4(7, 5, 9).
13. А1(3, 5, 4), А2(8, 7, 4), А3(5, 10, 4), А4(4, 7, 8).
14. А1(10, 9, 6), А2(2, 8, 2), А3(9, 8, 9), А4(7, 10, 3).
15. А1(1, 8, 2), А2(5, 2, 6), А3(5, 7, 4), А4(4, 10, 9).
16. А1(6, 6, 5), А2(4, 9, 5), А3(4, 6, 11), А4(6, 9, 3).
17. А1(7, 2, 2), А2(-5, 7, -7), А3(5, -3, 1), А4(2, 3, 7).
18. А1(8, -6, 4), А2(10, 5, -5), А3(5, 6, -8), А4(8, 10, 7).
19. А1(1, -1, 3), А2(6, 5, 8), А3(3, 5, 8), А4(8, 4, 1).
20. А1(1, -2, 7), А2(4, 2, 10), А3(2, 3, 5), А4(5, 3, 7).
21. А1(4, 2, 10), А2(1, 2, 0), А3(3, 5, 7), А4(2, -3, 5).
22. А1(2, 3, 5), А2(5, 3, -7), А3(1, 2, 7), А4(4, 2, 0).
23. А1(5, 3, 7), А2(-2, 3, 5), А3(4, 2, 10), А4(1, 2, 7).
24. А1(4, 3, 5), А2(1, 9, 7), А3(0, 2, 0), А4(5, 3, 10).
25. А1(3, 2, 5), А2(4, 0, 6), А3(2, 6, 5), А4(6, 4, -1).
26. А1(2, 1, 6), А2(1, 4, 9), А3(2, -5, 8), А4(5, 4, 2).
27. А1(2, 1, 7), А2(3, 3, 6), А3(2, -3, 9), А4(1, 2, 5).
28. А1(2, -1, 7), А2(6, 3, 1), А3(3, 2, 8), А4(2, -3, 7).
29. А1(0, 4, 5), А2(3, -2, 1), А3(4, 5, 6), А4(3, 3, 2).
30. А1(3, -1, 2), А2(-1, 0, 1), А3(1, 7, 3), А4(8, 5, 8).
Задание 1.6
Решить следующие задачи
1. Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку М (-2, 7, 3) параллельно плоскости х - 4 у + 5 z - 1 = 0. 2. Составить уравнение плоскости, проходящей через середину отрезка М 1 М 2 перпендикулярно к этому отрезку, если М 1(1, 5, 6), М 2(-1, 7, 10). 3. Найти расстояние от точки М (2; 0; -0,5) до плоскости 4 х - 4 у + 2 z + 17 = 0. 4. Составить уравнение плоскости, проходящей через точку А (2, -3, 5) параллельно плоскости Оху. 5. Составить уравнение плоскости, проходящей через ось Ох и точку А (2, 5, -1). 6. Составить уравнение плоскости, проходящей через точки А (2, 5, -1), В (-3, 1, 3) параллельно оси Оу. 7. Составить уравнение плоскости, проходящей через точку А (3, 4, 0) и прямую х - 2 = у - 3 = z + 1 . 1 2 2 8. Составить уравнение плоскости, проходящей через две параллельные прямые х - 3 = у = z - 1 и х + 1 = у - 1 = z. 2 1 2 2 1 2 9. Составить общие уравнения прямой, образованной пересечением плоскости 3 х - у - 7 z + 9 = 0 с плоскостью, проходящей через ось Ох и точку А (3, 2, -5). 10. Составить уравнение плоскости в <<отрезках>>, если она проходит через точку М (6, -10, 1) и отсекает на оси Ох отрезок а = -3, а на оси Оz - отрезок с = 2. 11. Составить уравнение плоскости, проходящей через точку А (2, 3, -4) параллельно двум векторам а = (4, 1, -1) и b = (2, -1, 2). 12. Составить уравнение плоскости, проходящей через точки А (1,1,0), В (2,-1,-1) перпендикулярно к плоскости 5 х + 2 у + 3 z -7= 0. 13. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к двум плоскостям 2 х - 3 у + z - 1 = 0 и х - у + 5 z +3 = 0. 14. Составить уравнение плоскости, проходящей через точки А (3, -1, 2), В (2, 1, 4) параллельно вектору а = (5, -2, -1). 15. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к вектору 16. Найти величины отрезков, отсекаемых на осях координат плоскостью, проходящей через точку М (2, -3, 3) параллельно плоскости 3 х + у - 3 z = 0. 17. Составить уравнение плоскости, проходящей через точку М (1, -1, 2) перпендикулярно к отрезку М 1 М 2, если М 1(2, 3, -4), М 2(-1, 2, -3).
18. Показать, что прямая х + 3 у - 2 z + 1 = 0, а прямая х = t + 7, у = t - 2, z = 2 t + 1 лежит в этой плоскости. 19. Составить общее уравнение плоскости, проходящей через точку А (3, -4, 1) параллельно координатной плоскости Охz. 20. Составить уравнение плоскости, проходящей через ось Оу и точку М (3, -5, 2). 21. Составить уравнение плоскости, проходящей через точки М (1, 2, 3) и N (-3, 4, -5) параллельно оси Оz. 22. Составить уравнение плоскости, проходящей через точку М (2, 3, -1) и прямую х = t - 3, у = 2 t + 5, z = -3 t + 1. 23. Найти проекцию точки М (4, -3, 1) на плоскость х - 2 у - z - 15 = 0. 24. Определить, при каком значении В плоскости х - 4 у + z - 1 = 0 и 2 х + Ву + 10 z - 3 = 0 будут перпендикулярны. 25. Составить уравнение плоскости, которая проходит через точку М (2, -3, -4) и отсекает на осях координат отличные от нуля отрезки одинаковой величины. 26. При каких значениях n и А прямая к плоскости Ах + 2 у - 2 z - 7 = 0? 27. Составить уравнение плоскости, проходящей через точки А (2, 3, -1), В (1, 1, 4) перпендикулярно к плоскости х - 4 у + 3 z + 2 = 0. 28. Составить уравнение плоскости, проходящей через начало координат перпендикулярно к плоскостям х + 5 у - z + 7=0 и 3 х - у + 2 z - 3=0. 29. Составить уравнение плоскости, проходящей через точки М (2, 3, -5) и N (-1, 1, -6) параллельно вектору а = (4, 4, 3). 30. Определить, при каком значении С плоскости 3 х - 5 у + Сz - 3 = 0 и х - 3 у + 2 z + 5 = 0 будут перпендикулярны.
Задание 1.7
Решить следующие задачи
1. Найти уравнение прямой, проходящей через точку пересечения прямых 3 х - 2 у - 7 = 0 и х + 3 у - 6 = 0 и отсекающей на оси абсцисс отрезок, равный 3. 2. Найти проекцию точки А (-8, 12) на прямую, проходящую через точки В (2, -3) и С (-5, 1). 3. Даны две вершины треугольника АВС: А (-4, 4), В (4, -12) и точка М (4, 2) пересечения его высот. Найти вершину С. 4. Найти уравнение прямой, отсекающей на оси ординат отрезок, равный 2, и проходящей параллельно прямой 2 у - х = 3. 5. Найти уравнение прямой, проходящей через точку А (2, -3) и точку пересечения прямых 2 х - у = 5 и х + у = 1. 6. Доказать, что четырёхугольник АВСD - трапеция, если А (3, 6), В (5, 2), С (-1, -3), D (-5, 5). 7. Записать уравнение прямой, проходящей через точку А (3, 1) перпендикулярно к прямой ВС, если В (2, 5), С (1, 0). 8. Найти уравнение прямой, проходящей через точку А (-2, 1) параллельно прямой MN, если М (-3, -2), N (1, 6). 9. Найти точку, симметричную точке М (2, -1) относительно прямой х - 2 у + 3 = 0. 10. Найти точку О пересечения диагоналей четырёхугольника АВСD, если А (-1, -3), В (3, 5), С (5, 2), D (3, -5). 11. Через точку пересечения прямых 6 х -4 у +5=0, 2 х +5 у+ 8=0 провести прямую, параллельную оси абсцисс. 12. Известны уравнения стороны АВ треугольника АВС 4 х + у = 12, его высот ВН 5 х - 4 у = 12 и АМ х + у = 6. Найти уравнения двух других сторон треугольника АВС. 13. Даны две вершины треугольника АВС: А (-6, 2), В (2, -2) и точка пересечения его высот Н (1, 2). Найти координаты точки М пересечения стороны АС и высоты ВН. 14. Найти уравнения высот треугольника АВС, проходящих через вершины А и В, если А (-4, 2), В (3, -5), С (5, 0). 15. Вычислить координаты точки пересечения перпендикуляров, проведенных через середины сторон треугольника, вершинами которого служат точки А (2, 3), В (0, -3), С (6, -3). 16. Составить уравнение высоты, проведённой через вершину А треугольника АВС, зная уравнения его сторон: АВ - 2 х - у - 3 = 0, АС - х + 5 у - 7 = 0, ВС - 3 х - 2 у + 13 = 0. 17. Дан треугольник с вершинами А (3, 1), В (-3, -1) и С (5, -12). Найти уравнение и вычислить длину его медианы, проведённой из вершины С. 18. Составить уравнение прямой, проходящей через начало координат и точку пересечения прямых 2 х + 5 у - 8 = 0 и 2 х + 3 у + 4 = 0. 19. Найти уравнения перпендикуляров к прямой 3 х + 5 у - 15 = 0, проведенных через точки пересечения данной прямой с осями координат. 20. Даны уравнения сторон четырехугольника: х - у = 0, х + 3 у = 0, х - у - 4 = 0, 3 х + у - 12 = 0. Найти уравнения его диагоналей. 21. Составить уравнения медианы СМ и высоты СК треугольника АВС, если А (4, 6), В (-4, 0), С (-1, -4). 22. Через точку Р (5, 2) провести прямую: а) отсекающую равные отрезки на осях координат; б) параллельную оси Ох; в) параллельную оси Оу. 23. Записать уравнение прямой, проходящей через точку А (-2, 3) и составляющей с осью Ох угол: а) 450; б) 900; в)00. 24. Какую ординату имеет точка С, лежащая на одной прямой с точками А (-6, -6) и В (-3, -1) и имеющая абсциссу, равную 3? 25. Через точку пересечения прямых 2 х - 5 у - 1 = 0 и х + 4 у - 7 = 0 провести прямую, делящую отрезок между точками А (4, -3) и В (-1, 2) в отношении l = 2/3. 26. Известны уравнения двух сторон ромба 2 х - 5 у - 1 = 0 и 2 х - 5 у - 34 = 0 и уравнение одной из его диагоналей х +3 у -6=0. Найти уравнение второй диагонали. 27. Найти точку Е пересечения медиан треугольника, вершинами которого являются точки А (-3, 1), В (7, 5) и С (5, -3). 28. Записать уравнения прямых, проходящих через точку А (-1, 1) под углом 450 к прямой 2 х + 3 у = 6. 29. Даны уравнения высот треугольника АВС 2 х -3 у +1=0, х + 2 у + 1 = 0 и координаты его вершины А (2, 3). Найти уравнения сторон АВ и АС треугольника. 30. Даны уравнения двух сторон параллелограмма х - 2 у = 0, х - у - 1 = 0 и точка пересечения его диагоналей М (3, -1). Найти уравнения двух других сторон.
Задание 1.8
Построить поверхности и определить их вид (название).
1. а) 4 х 2 - у 2 - 16 z 2 + 16 = 0; б) х 2 + 4 z = 0.
2. а) 3 х 2 + у 2 + 9 z 2 - 9 = 0; б) х 2 + 2 у 2 - 2 z = 0.
3. а) -5 х 2 + 10 у 2 - z 2 + 20 = 0; б) у 2 + 4 z 2= 5 х 2.
4. а) 4 х 2 - 8 у 2 + z 2 + 24 = 0; б) х 2 - у = -9 z 2.
5. а) х 2 - 6 у 2 + z 2 = 0; б) 7 х 2 - 3 у 2 - z 2= 21.
6. а) z = 8 - х 2 - 4 у 2; б) 4 х 2 + 9 у 2 + 36 z 2= 72.
7. а) 4 х 2 + 6 у 2 - 24 z 2 = 96; б) у 2 + 8 z 2= = 20 х 2.
8. а) 4 х 2 - 5 у 2 - 5 z 2 + 40 = 0; б) у = 5 х 2 + 3 z 2.
9. а) х 2 = 8(у 2 + z 2); б) 2 х 2 + 3 у 2 - z 2= 18. 10. а) 5 z 2 + 2 у 2 = 10 х; б) 4 z 2 - 3 у 2 - 5 х 2 + 60 = 0.
11. а) х 2 - 7 у 2 - 14 z 2 - 21 = 0; б) 2 у = х 2 + 4 z 2.
12. а) 6 х 2 - у 2 + 3 z 2 - 12 = 0; б) 8 у 2 + 2 z 2 = х.
13. а) -16 х 2 + у 2 + 4 z 2 - 32 = 0; б) 6 х 2 + у 2 - 3 z 2 = 0.
14. а) 5 х 2 - у 2 - 15 z 2 + 15 = 0; б) х 2 + 3 z = 0.
15. а) 6 х 2 + у 2 + 6 z 2 - 18 = 0; б) 3 х 2 + у 2 - 3 z = 0.
16. а) -7 х 2 + 14 у 2 - z 2 + 21 = 0; б) у 2 + 2 z 2 = 6 х 2.
17. а) -3 х 2 + 6 у 2 - z 2 - 18 = 0; б) х 2 - 2 у = - z 2.
18. а) 4 х 2 - 6 у 2 + 3 z 2 = 0; б) 4 х 2 - у 2 - 3 z 2 = 12.
19. а) z = 4 - х 2 - у 2; б) 3 х 2 + 12 у 2 + 4 z 2 = 48.
20. а) 4 х 2 + 5 у 2 - 10 z 2 = 60; б) 7 у 2 + z 2 = 14 х 2.
21. а) 9 х 2 - 6 у 2 - 6 z 2 + 1 = 0; б) 15 у = 10 х 2 + 6 у 2.
22. а) х 2 = 5 (у 2 + z 2); б) 2 х 2 + 3 у 2 - z 2 = 36.
23. а) 4 х 2 + 3 у 2 = 14 х; б) 3 х 2 - 4 у 2 - 2 z 2 + 12 = 0.
24. а) 8 х 2 - у 2 - 2 z 2 - 32 = 0; б) у - 4 z 2 = 3 х 2.
25. а) х 2 - 6 у 2 + z 2 - 12 = 0; б) х - 3 z 2 = 9 у 2.
26. а) 2 х 2 - 3 у 2 - 5 z 2 + 30 = 0; б) 2 х 2 + 3 z = 0.
27. а) 7 х 2 + 2 у 2 + 6 z 2 - 42 = 0; б) 2 х 2 + 4 у 2 - 5 z = 0.
28. а) -4 х 2 + 12 у 2 - 3 z 2 + 24 = 0; б) 2 у 2 + 6 z 2 = 3 х.
29. а) 3 х 2 - 9 у 2 + z 2 + 27 = 0; б) z 2 - 2 у = -4 х 2.
30. а) 27 х 2 - 63 у 2 + 21 z 2 = 0; б) 3 х 2 - 7 у 2 - 2 z 2 = 42.
К о н т р о л ь н а я р а б о т а № 2
Дифференцирование и исследование функций
Задание 2.1
Найти 1.
2.
3.
4.
5.
6.
7.
8.
9. 10.
12.
13.
14.
15.
18.
22.
27.
28.
29.
30.
Задание 2.2
Найти
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
|

 ), А 2(
), А 2(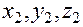 ), A3(
), A3( ) и А 4(
) и А 4(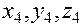 ). Составить уравнения:
). Составить уравнения: , если А (5, -2, 3), В (1, -3, 5).
, если А (5, -2, 3), В (1, -3, 5). параллельна плоскости
параллельна плоскости перпендикулярна
перпендикулярна .
. .
. .
.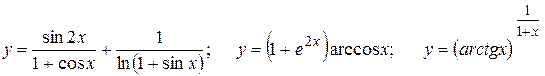 .
. .
. .
. .
. .
. .
.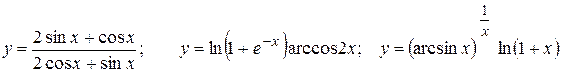 .
. .
.
 .
. .
. .
. .
.

 .
.