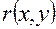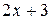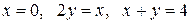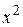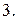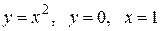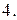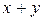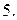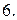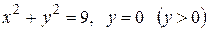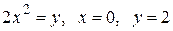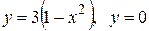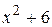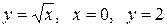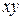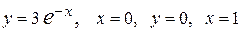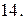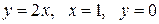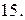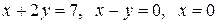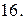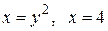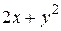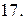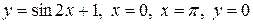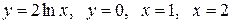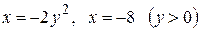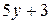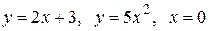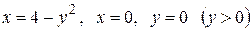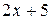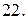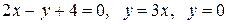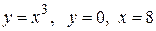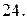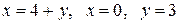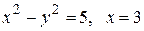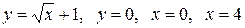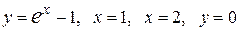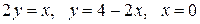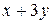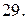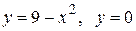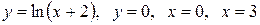Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М., 1980. 4 страница
КОНТРОЛЬНАЯ РАБОТА № 4.
Интегральное исчисление.
Задача 4.1
С помощью интегрирования по частям вычислить неопределённый интеграл от функции вида
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Задача 4.2.
Вычислить неопределённый интеграл с помощью разложения на простейшие дроби подинтегральной функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Задача 4.3.
Вычислить с помощью подстановки неопределённый интеграл от функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Задача 4.4.
Вычислить с помощью подстановки неопределённый интеграл от функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Задача 4.5.
Вычислить площадь фигуры, ограниченной линиями:
Задача 4.6.
Переходя в полярную систему координат
первым витком спирали Архимеда
одним лепестком линии
кардиоидой
12. одним лепестком линии
13. четырёхлепестковой розой 14. лемнискатой Бернулли первым и вторым витками спирали Архимеда оси окружностью 17. 18.
22. 23.
25. 26. 27. 28. 29.
Задача 4.7.
Вычислить несобственный интеграл или доказать его сходимость
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Задача 4.8.
Вычислить массу неоднородной пластины
|

 16.
16. 
 17.
17. 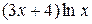
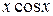 18.
18. 
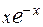 19.
19. 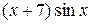
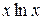 20.
20. 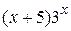
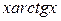 21.
21. 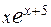
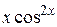 22.
22. 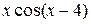
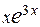 23.
23. 
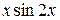 24.
24. 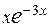
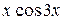 25.
25. 
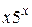 26.
26. 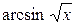
 27.
27. 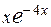
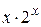 28.
28. 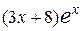
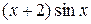 29.
29. 
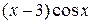 30.
30. 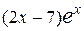
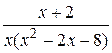 16.
16. 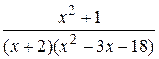
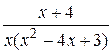 17.
17. 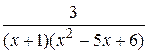
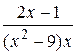 18.
18. 
 19.
19. 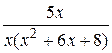
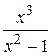 20.
20. 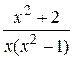
 21.
21. 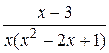
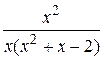 22.
22. 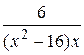
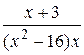 23.
23. 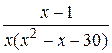
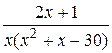 24.
24. 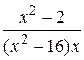
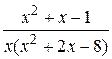 25.
25. 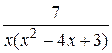
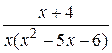 26.
26. 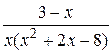
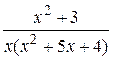 27.
27. 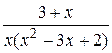
 28.
28. 
 29.
29. 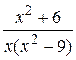
 30.
30. 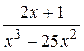
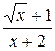 16.
16. 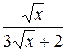
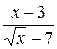 17.
17. 
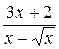 18.
18. 
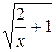 19.
19. 
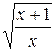 20.
20. 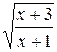
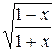 21.
21. 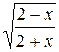
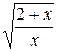 22.
22. 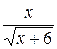
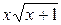 23.
23. 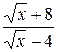
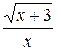 24.
24. 
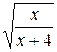 25.
25. 
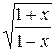 26.
26. 
 27.
27. 
 28.
28. 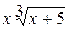
 29.
29. 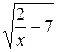
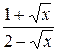 30.
30. 
 16.
16. 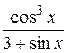
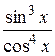 17.
17. 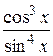
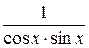 18.
18. 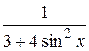
 19.
19. 
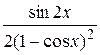 20.
20. 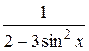
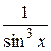 21.
21. 
 22.
22. 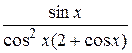
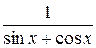 23.
23. 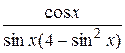
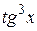 24.
24. 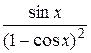
 25.
25. 
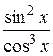 26.
26. 
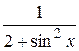 27.
27. 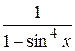
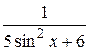
 29.
29. 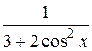
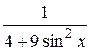 30.
30. 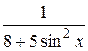
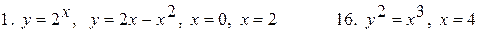














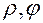 вычислить с помощью опре-деленного интеграла площадь, ограниченную кривыми:
вычислить с помощью опре-деленного интеграла площадь, ограниченную кривыми: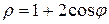
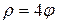 и отрезком полярной оси
и отрезком полярной оси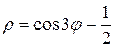
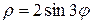

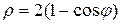 и окружностью
и окружностью 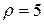
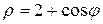
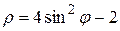

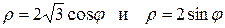
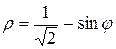



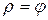 и отрезком полярной
и отрезком полярной и прямой
и прямой 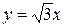
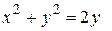 и
и 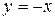 (большая часть)
(большая часть)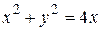 и
и 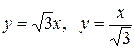
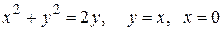
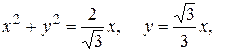 (большая часть)
(большая часть)
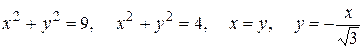 (меньшая часть)
(меньшая часть)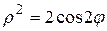 и
и 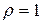
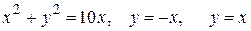
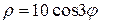 и
и  (меньшая часть)
(меньшая часть) (вне окружности)
(вне окружности)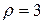 и первого лепестка линии
и первого лепестка линии 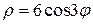
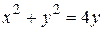 между прямыми
между прямыми 
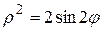
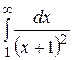 16.
16. 
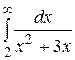 17.
17. 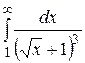
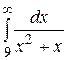 18.
18. 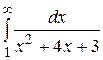
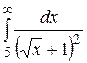 19.
19. 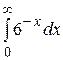
 20.
20. 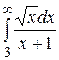
 21.
21. 

 22.
22. 
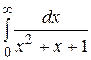 23.
23. 
 24.
24. 
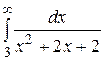 25.
25. 
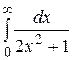 26.
26. 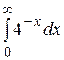
 27.
27. 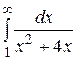
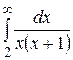 28.
28. 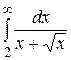
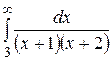 29.
29. 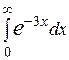
 30.
30. 
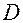 , ограниченной заданными линиями и имеющей поверхностную плотность
, ограниченной заданными линиями и имеющей поверхностную плотность